Sorting algorithm 2: Selection Sort

for i <- 0 to n-1
	pos <- i
	for j <- i+1 to n-1
		if (arr[j] < arr [pos])
			pos = j;
	end for of j
	
	swap arr[i], arr[pos];

end for of i.

2.4 Understanding Selection Sort with an example

Consider the array: [4, 6, 1, 34, 21, 14]

Pass 1:

Initially, we need to fill the index 0, with the smallest element. We first check the array. We see that 1 is the least element and it is in index 2. Hence swap at index 0 and index 2. Below is the result.

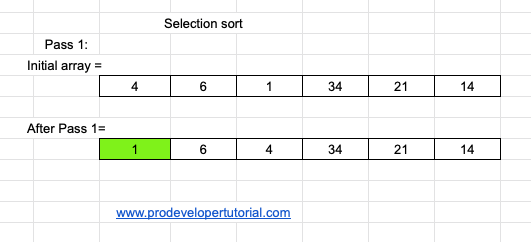
Pass 2:

As we have already placed lowest element in index 0, now we need to place 2nd lowest element.
From the array we can see that 4 is the 2nd lowest element. Hence swap the elements at index 1 and index 2, as shown below:

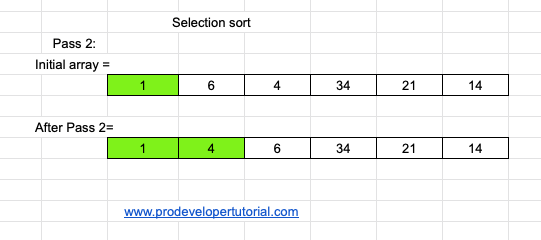
Pass 3:

At pass 3, we can see that element 6 is in it’s correct position. Hence we don’t do anything in this pass.

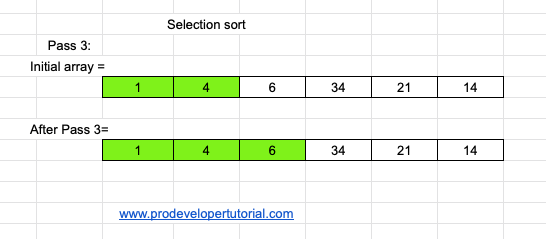
Pass 4:

At pass 4, we swap the elements 34 and 14.

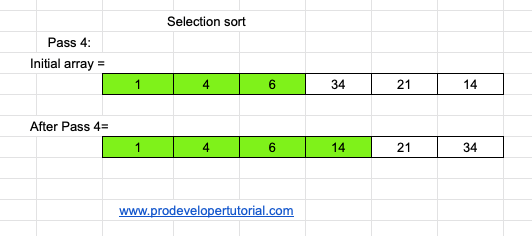
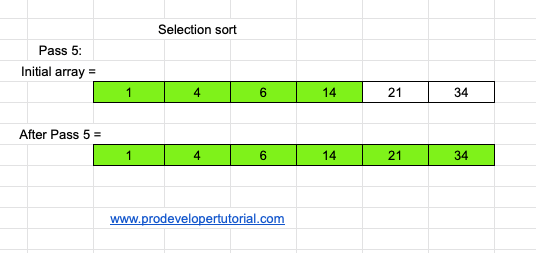
Pass 5 :

As you can see that the array is already sorted. Hence we do nothing.

2.5 Implementation of Selection Sort in C

#include<stdio.h>

void print_array(int array[], int length)
{
	int index = 0;

	printf("The sorted array is \n");

	for(index = 0 ; index < length ; index++)
	{
		printf("%d\n",array[index] );
	}
}
void swap (int *num_1, int *num_2)
{
	int temp = *num_1;
	*num_1 = *num_2;
	*num_2 = temp;
}

void selection_sort (int array[], int length)
{
	int outer_loop_index = 0;
	int inner_loop_index = 0;
	int position = 0;

	for(outer_loop_index = 0; outer_loop_index < length - 1; outer_loop_index ++)
	{
		position = outer_loop_index;

		for(inner_loop_index = outer_loop_index+1 ; inner_loop_index < length ; inner_loop_index ++)
		{
			if(array [inner_loop_index] < array[position])
			{
				position = inner_loop_index;
			}
		}
				swap(&array[outer_loop_index], &array [position]);
	}
}

int main()
{
	int length = 0;
	int array[100];
	int index = 0;

	printf("Enter the length of the array\n");
	scanf("%d", &length);

	printf("Enter the array elements of length %d\n", length);

	for (index = 0; index < length; ++index)
	{
		scanf("%d", &array[index]);
	}

	selection_sort(array, length);

	print_array(array, length);


}

2.6 Output of the program

Enter the length of the array
5

Enter the array elements of length 5

5
4
3
2
1

The sorted array is
1
2
3
4
5

2.7 Time complexity analysis of Selection Sort

As we are comparing the elements as:

(n-1) + (n-2) + . . . . + 2 + 1 
(n(n-1))/2
O(n^2)

Here Best case, worst case, average case is O(n^2).