Minimum Spanning Tree tutorial 2: Introduction to Kruskal’s algorithm

In this chapter we shall learn about below topics:

Kruskal’s algorithm is used to find MST in a graph. It is a greedy based algorithm.

Why do we call it as greedy? Because, as you will see further, we choose the shortest distance first without considering the fact what there might be more optimized path. Hence, we find another path with shortest value, we update the result with that value.

Let us first understand the working of the algorithm, then we shall solve with the help of an example.

The working of Kruskal’s algorithm is very simple and can be understood by 3 simple steps as given below:

Step 1: Sort all the edges according to their weights.

Step 2: a. Start from the edge with smallest weight and connect them together.

Before connecting, check if it forms a cycle if it forms a cycle then reject the edge and go for the net smallest weighted edge.

Step 3: Check if all the vertices are connected. If they are not connected, then repeat step 2 till all the vertices are connected.

Once all the tree vertices are connected to an edge, we get MST.

Note: As you see in Prims algorithm that starts by choosing a root vertex, in Kruskal’s algorithm we start connecting 2 vertices by choosing least weighted edges.

Consider the graph as below

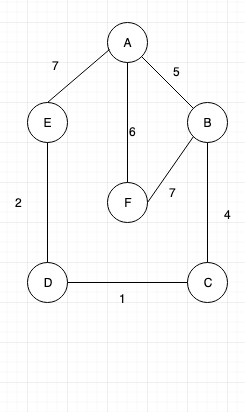
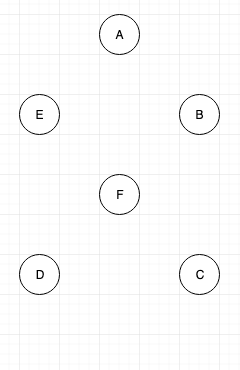
Initial Configuration will be as below:

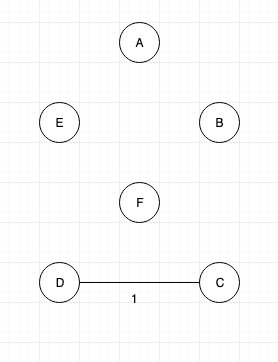
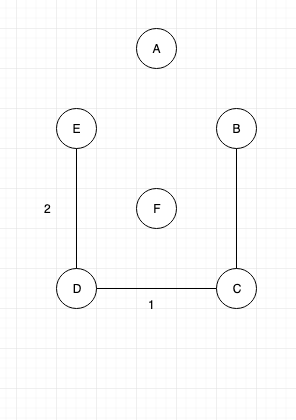
Connect the nodes “C” and “D” as their weight is minimum

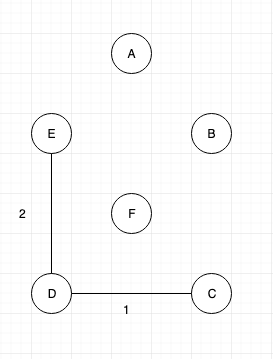
Next connect nodes “D” and “E”, as they are next minimum

Next connect “C” and “B”, as they are next minimum

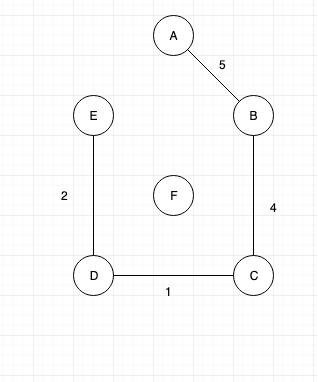
Next connect “B” and “A”

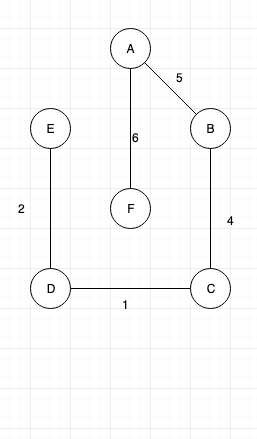
Next connect “A” and F”. Thus connecting all the nodes and forming a MST.

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<vector>

using namespace std;

#define MAX 1000

struct edge
{

	int u, v, w;
};

typedef struct  edge E;

int parents[MAX+5];
vector <E> graph; // Store the inputted graph (u, v, w).
vector <E> selected_edges; // Store the edges which is selected for the MST from given graph.

bool comp (const E& l, const E& r)
{

	return l.w < r.w;
}

void make_set(int nodes)
{

	for(int i=1; i<=nodes; i++)
		parents[i] = i;

	return;
}

int findParent( int r )
{

	if( r == parents[r] ) return r;

	return parents[r] = findParent( parents[r] );
}


int Kruskal_MST (int nodes)
{

	make_set(nodes);

	sort(graph.begin(), graph.end(), comp);

	int edgeCounter=0, totalCost=0;

	int len = graph.size();
	
	for(int i=0; i<len; i++)
	{

		int parent_of_u = findParent( graph[i].u );
		int parent_of_v = findParent( graph[i].v );

		if( parent_of_u != parent_of_v )
		{

			parents[ parent_of_u ] = parent_of_v;
			totalCost += graph[i].w;
			selected_edges.push_back( graph[i] );

			edgeCounter++;
			if( edgeCounter == nodes-1 )
				break;
		}

	}

	return totalCost;
}




int main()
{
	E getEdge;
	int nodes, edges;

	cout<<"How many nodes: "<<endl;
	cin >> nodes;

	cout<<"How many edges: "<<endl;
	cin >> edges;

	cout<<"Enter 2 nodes & their costs (u v & w): \n";
	
	for(int i=1; i<=edges; i++)
	{

		int u, v, w;
		cout<<"Edge "<< i<<endl;
		cin >> u >> v >> w;

		getEdge.u = u; 
		getEdge.v = v; 
		getEdge.w = w;

		graph.push_back(getEdge);
	}

	int totalCost = Kruskal_MST(nodes); 
	
	cout<<"\n\nSelected Edges and their costs: \n";
	
	for(int i=0; i<selected_edges.size(); i++)
	{		
		cout<<"Edge "<< i+1 <<":"<< selected_edges[i].u<< " -> " << selected_edges[i].v<< ": cost "<< selected_edges[i].w <<endl;
	}

	cout<<"\nTotal Costs: "<< totalCost<<endl;

	getchar();
	return 0;
}

Time complexity of Kruskal’s algorithm is O(logV)

Kruskal’s algorithm should be used in typical situations (sparse graphs) because it uses simpler data structures.