Minimum Path Sum in CPP

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.
Note: You can only move either down or right at any point in time.

Example:

Input:
[
[1,3,1],
[1,5,1],
[4,2,1]
]

Output: 7

Explanation: Because the path 1→3→1→1→1 minimizes the sum.

This problem can be solved with the help of Dynamic Programming.

We take a new (m * n) array. Then we shave the values by computing using a formula.

Let us understand the problem with the help of an example:

Consider the below array:

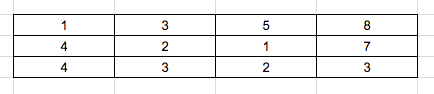
Here we need to find the minimum sum/cost from top right corner to bottom left corner. We can only move to right or move bottom.

Consider that we want to find the path for the highlighted image below:

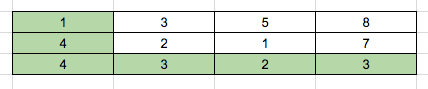
The total cost will be “1 + 4 + 4 + 3 + 2 + 3 = 17”.

But we need to find the min cost.

We shall solve by taking another array to calculate and store the values. Initialize arr[0][0] to 1, because it is the first path and can only be reached by cost 1.

Now we shall solve the first row.

To reach arr[0][1] there is only 1 way, from arr[0][0]. Hence the total cost will be “1 + 3 = 4”.
To reach arr[0][2] there is only 1 way, from arr[0][1]. Hence the total cost will be “1 + 3 + 5 = 9”.
To reach arr[0][3] there is only 1 way, from arr[0][2]. Hence the total cost will be “9 + 8 = 17”.

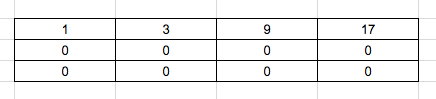
Now we solve 1st column

To reach arr[1][0] there is only 1 way, from arr[0][0]. Hence the total cost will be “1 + 4 = 5”.
To reach arr[2][0] there is only 1 way, from arr[0][1]. Hence the total cost will be “5 + 4 = 9 5”.

Now coming to 1st row:
To reach arr[1][1] there is only 2 ways, from arr[0][1] or arr[1][0]. But we need to take the minimum path. Hence we take the min cost of both the ways. i.e min(5, 4). The min cost is 4, we add it with present cost. Hence the total cost is 6.

To reach arr[1][2] there is only 2 ways, from arr[0][2] or arr[1][1]. But we need to take the minimum path. Hence we take the min cost of both the ways. i.e min(6, 9). The min cost is 6, we add it with present cost. Hence the total cost is 7.

Similarly arr[1][3] will be 14.

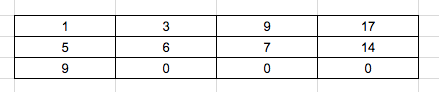
After solving the last row, the result is highlighted as shown below:

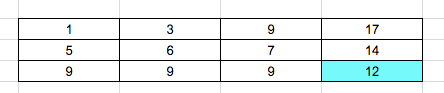
12 is the final result.

Hence from the above analysis we can come to an conclusion:

The cost of arr[i][j] = arr[i][j] + min(arr[i – 1][j], arr[i][j – 1]);

Solution in C++

/*
* File     : min_path_sum.cpp
* Author   : ajay.thousand@gmail.com
* Copyright: @ prodevelopertutorial.com
*/

#include<iostream>
#include<vector>

using namespace std;



int get_min_path(vector<vector<int>>& input) 
{
	//get the row size
	int m = input.size();

    //get the column size
	int n = input[0].size(); 

	//Create a 2D array and initialize it with 1
	vector<vector<int> > result(m, vector<int>(n, input[0][0]));

//Solve first row
	for (int i = 1; i < m; i++)
		result[i][0] = result[i - 1][0] + input[i][0];

//Solve first column
	for (int j = 1; j < n; j++)
		result[0][j] = result[0][j - 1] + input[0][j];

	for (int i = 1; i < m; i++)
		for (int j = 1; j < n; j++)
			result[i][j]  = min(result[i - 1][j], result[i][j - 1]) + input[i][j];

		return result[m - 1][n - 1];
	}

int main()
{
	//Declare 2D vector
	int row = 3;
	int column = 4;
	vector<vector<int> > input = { { 1, 3, 5, 8 },
                                   { 4, 2, 1, 7 },
                                   { 4, 3, 2, 3 },
                                  };

    cout<< "The input array is "<<endl;

    for (int i = 0; i < input.size(); i++)
    {
    	for (int j = 0; j < input[0].size(); j++)
    	{
    		cout<< input[i][j]<<" ";
    	}
    	cout<<endl;
    }

    cout<< "\nThe min path is =  "<<get_min_path(input)<<endl;

	return 0;
}

Output:

1 3 5 8
4 2 1 7
4 3 2 3

The min path is = 12