Job Sequencing with deadline Problem

In this tutorial we shall learn about job sequencing with deadline problem. We shall solve this problem with the help of Greedy Approach.

Problem statement:

You are given a set of jobs associated with deadline and profits attached to the jobs. Your goal is to find the maximum profit within the given deadline.

You have to assume, only one job can run at a time. Profits will be counted only after the execution of that task is completed. Every job needs one unit of time.

The deadline that is mentioned, is the amount of time a job is willing to wait.

Given below are number of jobs and deadline and profit associated with it.

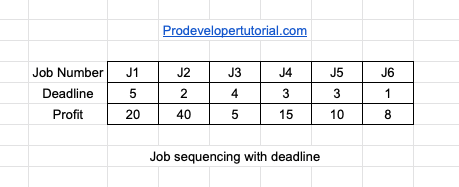
Now, our focus is on the profits, hence we shall sort them accordingly to the profits

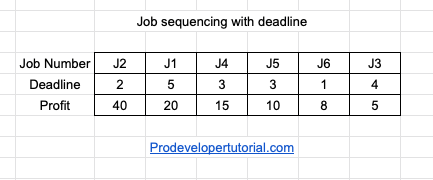
Now we have applied greedy method. Because we want to get more profits, hence we sort according to decreasing profits.

Here the maximum deadline is 5. Hence we create 5 slots.

0 _ 1 _ 2 _ 3 _ 4 _ 5 Profit = 0.

Here the slots are

0 _ 1,

1 _ 2,

2 _ 3,

3 _ 4,

4 _ 5

So for job j2, it is willing to wait till 2 nd slot. Hence we take that slot and profit is 40.


0 _ 1,

1 _ 2 = taken by J2

2 _ 3,

3 _ 4,

4 _ 5

Profit = 40

For job J1, it is willing to wait till 5. Hence take that slot.

0 _ 1,

1 _ 2 = taken by J2

2 _ 3,

3 _ 4,

4 _ 5 = taken by J1

Profit = 40 + 20 = 60


Now for job J4, it is willing to wait till 3. Hence we will put it in that slot and profit increases.

0 _ 1,

1 _ 2 = taken by J2

2 _ 3 = taken by J4

3 _ 4,

4 _ 5 = taken by J1

Profit = 40 + 20 + 15 = 75

Now for job J5. It is also willing to wait 3 time units. But the slot 2_3 is already taken.

But check if there are any earlier time slots available?

Yes, there is a slot available at 0_1. Here, for any task, if there is a deadline, it means that you cannot perform that task after that deadline, but you can perform before it. Hence for the job J5, we take the slot 0_1 slot and get the profit.

0 _ 1 = taken by J5

1 _ 2 = taken by J2

2 _ 3 = taken by J4

3 _ 4,

4 _ 5 = taken by J1

Profit = 40 + 20 + 15 + 10 = 85


Now for the job J6.

J6 can only wait for 1-time unit. But that slot 0_1 has been taken by J5. Hence discard job J6.

Now for the job J3. This job is willing to wait 5 time units. The slot 3_4 is available. Hence we execute the job in that time slot.


0 _ 1 = taken by J5

1 _ 2 = taken by J2

2 _ 3 = taken by J4

3 _ 4 = taken by J3

4 _ 5 = taken by J1


Profit = 40 + 20 + 15 + 10 + 5 = 90

Hence our solution.

Solution for Job sequencing with deadline problem in C++

#include <iostream>

using namespace std;

//structure to hold job details
struct Job 
{
	char id;
	int deadline;
	int profit;
};

// to get higher profit of 2 jobs
bool comparator (Job a, Job b) 
{
	return (a.profit > b.profit);
}

void printJobScheduling (Job arr[], int n) 
{
	//sorting according to profit in ascending order
	sort (arr, arr+n, comparator);
	int result[n];
	bool slot[n];

	// initialize result array and slot array
	for (int i = 0; i < n; i++) 
	{
		slot[i] = false;
		result[i] = -1;
	}

	//calculate the jobs according to profit
	for (int i = 0; i < n; i++) 
	{
		for (int j = min(n, arr[i].deadline) - 1; j >= 0; j--) 
		{
			if (!slot[j]) {
				result[j] = i;
				slot[j] = true;
				break;
			}
		}
	}

	//print the solution
	for (int i = 0; i < n; i++) 
	{
		if (slot[i]) 
		{
			cout << arr[result[i]].id << "\t";
		}
	}
	cout << endl;
}

int main (void) 
{
	Job arr[6] = {
		{'j1', 5, 20}, 
		{'j2', 2, 40}, 
		{'j3', 4, 5}, 
		{'j4', 3, 15}, 
		{'j5', 3, 10},
		{'j6', 1, 8}
	};
	
	cout << "Result = " << endl;
	printJobScheduling (arr, 6);
	return 0;
}

Output:

Result =
5	2	4	3	1