Hamming Distance

Consider 8 and 1

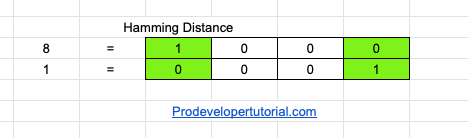
As highlighted in the image, there are 2 positions where the bits are different. Hence output should be 2.

We shall solve this by bit manipulation.

Before solving the problem, we need to understand 2 concepts

1. XOR

2. Brian Kernighan’s Algorithm

1. XOR

The truth table of xor is as below:

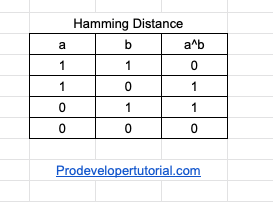
As you can see that XOR returns true if 2 bits are different. When 2 bits are same it will return 0. This is what we need for our solution.

Now that when we XOR 2 numbers, we get numbers of set bits that are different in their binary form.

Now we need to calculate/count the number of set bits.

This can be achieved by using Brian Kernighan’s Algorithm.

This algorithm works on below 2 steps:

1. Subtract 1 from the number will flip all the rightmost set bit.

2. and using bitwise & operator with (n) &(n-1) will remove the rightmost set bit from n.

i.e consider 10 in binary is 1 0 1 0

subtract                                         -1

Result = 1001 i.e 9.

When we do (1010 & 1001) we get 1000.

Similarly, we continue like this till we get the count of set bits of number 10.

Method 2:

We can also solve this problem with help of library function available in C++ as below:

bitset<32>(x^y).count();

#include<iostream>
using namespace std;

int hamming_distance_xor(int x, int y) 
{
    int count = 0, n = x ^ y;
    while (n) {
        ++count;
        n &= n - 1;
    }
    return count;
}


int hamming_distance_library(int x, int y) 
{
      return bitset<32>(x^y).count();
}

int main()
{
    int num_1 = 8;
    int num_2 = 1;

    cout<<"Hamming distance using xor is = "<<hamming_distance_xor(num_1, num_2)<<endl;
    cout<<"Hamming distance using library function is = "<<hamming_distance_library(num_1, num_2)<<endl;
}