Graph data structure tutorial 4. Graph Traversal

In the previous chapter we learnt about tree traversal. In this chapter we shall learn about graph traversal.

Graph traversal can be done in 2 ways:

As the name suggests, we take a node and follow deep in the node and then stop if we reach a dead end. Then we backtrack to the starting node and then check if there are other nodes that are left out.

Let us understand with the help of a graph below:

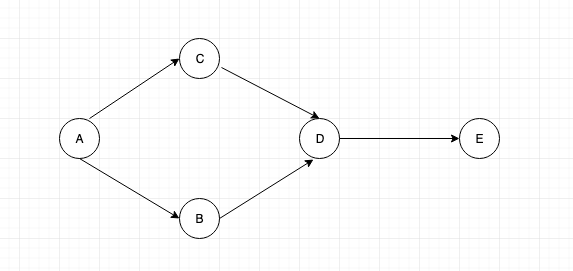
Now, let’s select a starting node. Let it be “A”. You can select any starting node.

From “A” we ca either go to node “C” or node “B”. We shall go to node “C”. Mark that node as visited [in green].

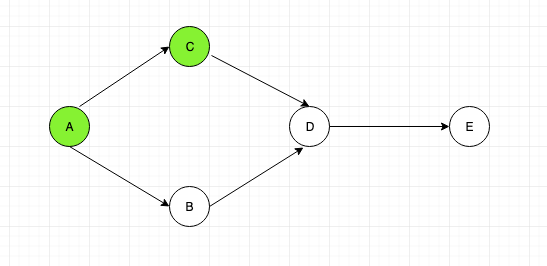
From “C” we can go to node “D”, Then from node “D” to node “E”.

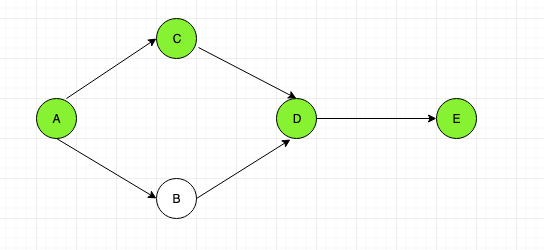
Now we have reached at the end. Hence we backtrack to the previous node and check if there are any other nodes that have not been visited. As only node that is unvisited is “B”, we backtrack till “A”.

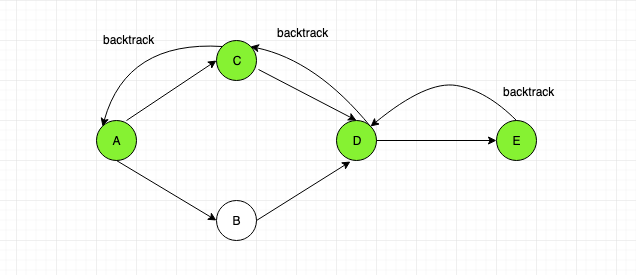
Now, from “A” we see that node “B” has not been visited . then visit it.

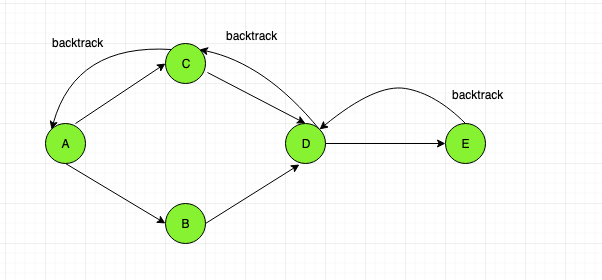
Hence the final result will be

A               C               D               E                B

Consider another example:

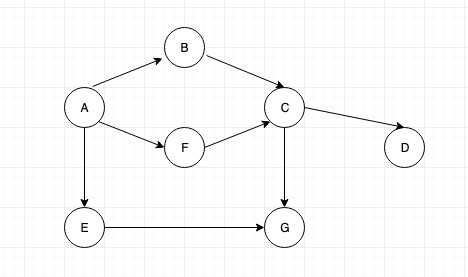
So initially we shall start with node “A”, then traverse to node “B” then to “C” then to “D”.

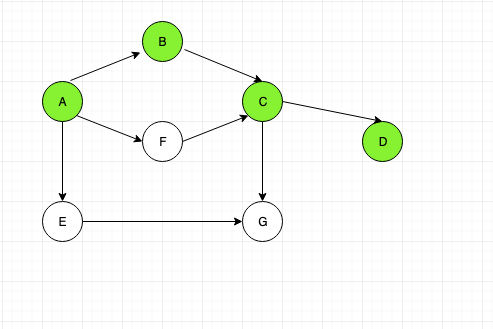
Then backtrack to “C”, now “G” node is unvisited. Visit it.

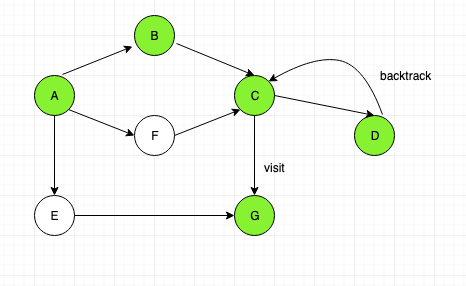
Now backtrack to node “G” to “C” to “B” to “A”. Then visit “F”.

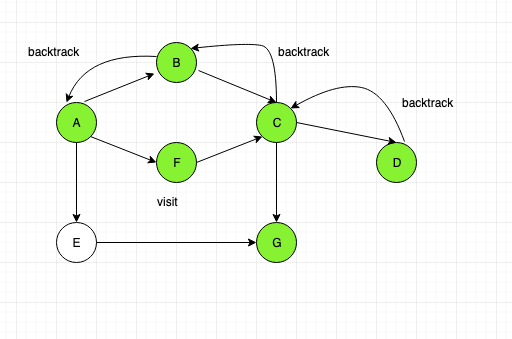
Now again backtrack to “A”, then visit “E”.

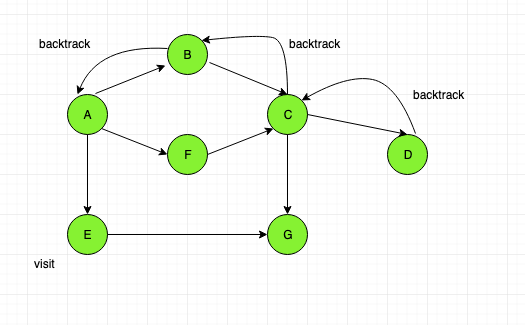
The order of nodes visited are:

A, B, C, D, G, F, E

Points to remember about DFS.

1. DFS is used to know if 2 nodes have a path between them.

2. We can only backtrack with the path that we have already visited.

3. If there is a node that cannot be reached, then we need to restart the graph traversal from that path.

For example:

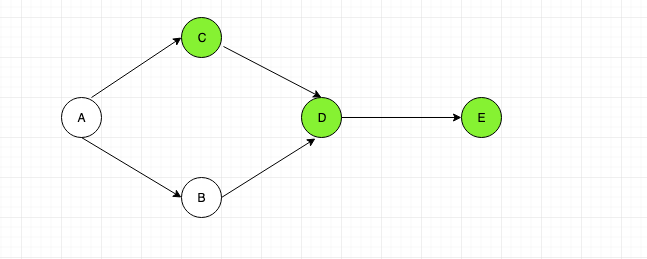
Here as we have started the traversal from Node “C, we cannot reach “A” and “B”. hence we restart the traversal from “A” then reach “B”.

Hence the traversal will be:

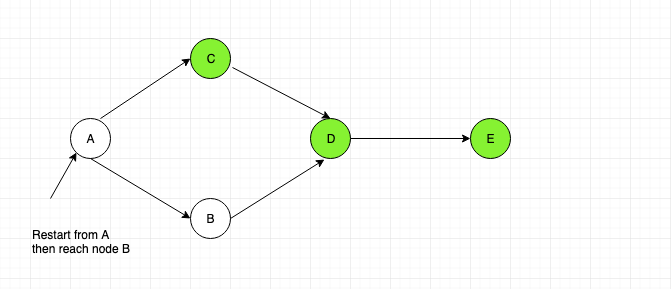
The path will be:

C               D               E                A               B

4. Stack Data structure is used to realize graph traversal using DFS.

In previous section we have looked at graph traversal using DFS. In this section we shall look at graph traversal using BFS.

In Breadth First Search traversal we go level by level. Consider the example below:

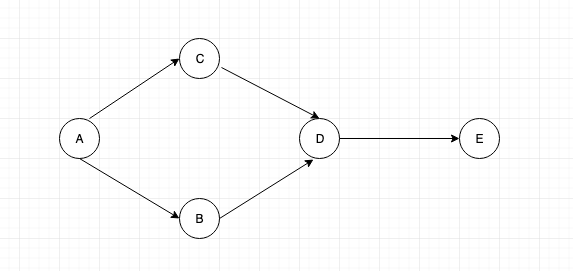
Now if we consider level by level, we can traverse it as below:

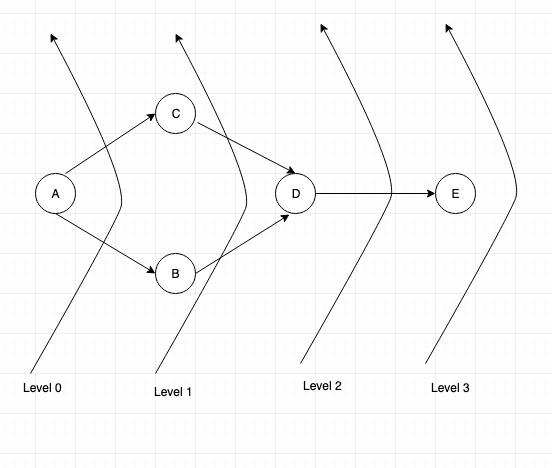
Hence the output will be

A               C               B               D               E

Points to remember for BFS.

1. BFS is used to find the shortest path between 2 nodes

2. BFS is realized using queue.