Given a collection of candidate numbers and a key, find all unique combinations in candidates where the candidate numbers sums to target.

Each number in candidates may only be used once in the combination.

Note:

• All numbers (including target) will be positive integers.
• The solution set must not contain duplicate combinations.

Example 1:

Input: candidates = [10,1,2,7,6,1,5], target = 8,
A solution set is:
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

Example 2:

Input: candidates = [2,5,2,1,2], target = 5,
A solution set is:
[
  [1,2,2],
  [5]
]

Before going through this solution, I suggest you please go through “Combination Sum 1”. In that post I have explained the concept of backtracking, that will be helpful for understanding the solution for this problem.

Given an array of n integers and an integer “key”, find three integers in the array such that the sum is closest to key.

The solution for this problem can be done in 2 ways:
1. Backtracking
2. DFS

In this post we shall go through DFS solution. As we have covered “backtracking” in “combination sum” problem.

So DFS, Depth First Search Solution. This solution is very easy to understand.

Here we go deep into the tree, first by taking 1 element, then adding with the next element.

If the sum of the elements is equal to the key, we save it in the array.

else if sum of the elements is less than the key, we add next number.

else if the sum of the elements gets greater than the key, we stop adding new elements, go back a step behind then add next number.

Let us understand the concept with the help of an example.

Input [2, 3, 1, 1] Key = 3

Step 1 is to sort the array:
[1, 1, 2, 3]

Below is the DFS solution visualization:

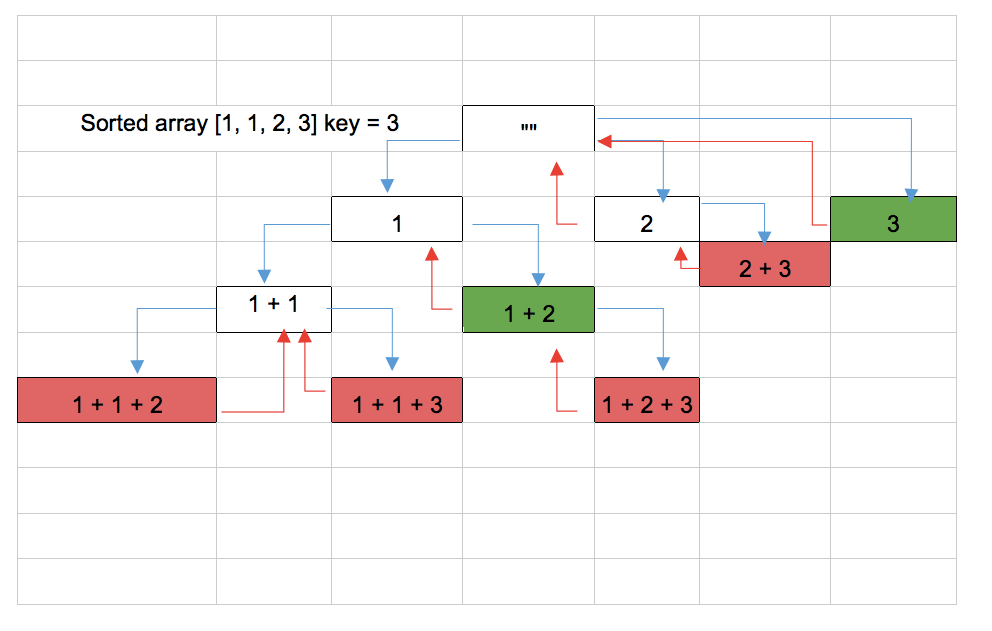
Initially we start with an empty set “”.

Then we start adding elements one by one.

First we add only “1”. Then we add “1 + 1” it is not equal to the key. Then add “1 + 1 + 2” as the sum is greater than key[represented in red box], we go one step up and then add remaining elements.

So while adding the elements, if any of sum of the set value is equal to the key, we store it and again find different sets.

Solution in C++

/*
* File     : combination_sum_2.cpp
* Author   : prodevelopertutorial.com
* Purpose  : To find all the number combination equal to the key
* Copyright: @ prodevelopertutorial.com
*/

#include<iostream>
#include <vector>

using namespace std;

vector<vector<int> > final_result_set;


void dfs_solution(vector<int> &input_set, vector<int>& temp_result_set, int key, int total_sum, int beg) 
{
    if (total_sum == key) 
    {
        final_result_set.push_back(temp_result_set);
        return;
    }

    if (total_sum > key || beg == input_set.size()) 
        return;
        
    temp_result_set.push_back(input_set[beg]);
        
    dfs_solution(input_set, temp_result_set, key, total_sum + input_set[beg], beg+1);
    temp_result_set.pop_back();

    int end = beg;
    while(end+1<input_set.size() && input_set[end]==input_set[end+1]) end++;

    dfs_solution(input_set, temp_result_set, key, total_sum, end+1);
}


vector<vector<int> > combinationSum_2_dfs_soluntion(vector<int>& input_set, int key) 
{

    vector<int> temp_result_set;
    
    sort(input_set.begin(), input_set.end());
    
    dfs_solution(input_set, temp_result_set, key, 0, 0);
    
    return final_result_set;

}

int main()
{
    vector<int> input_set;
    input_set.push_back(10);
    input_set.push_back(1);
    input_set.push_back(2);
    input_set.push_back(7);
    input_set.push_back(6);
    input_set.push_back(1);
    input_set.push_back(5);

    int key = 8;
     
    vector<vector<int> > final_set =  combinationSum_2_dfs_soluntion(input_set, key);

    // If final_set is empty, then
    if (final_set.size() == 0)
    {
        cout << "No possible combinations found";
        return 0;
    }
 
    // print the output
    for (int i = 0; i < final_set.size(); i++)
    {
        if (final_set[i].size() > 0)
        {
            cout << " ( ";
            for (int j = 0; j < final_set[i].size(); j++)
                cout << final_set[i][j] << " ";
            cout << ")";
        }
        cout<<endl;
    }

    return 0;
}

Output:

( 1 1 6 )
( 1 2 5 )
( 1 7 )
( 2 6 )