Finding shortest path algorithm tutorial 2. Introduction to Dijkstra’s Algorithm

In this chapter we shall learn about below topics:

In this tutorial we shall learn about Dijkstra’s algorithm. It is used to get single source shortest path algorithm.

You are given a weighted graph and you are given a source. You need to find shortest path from source vertex to every other vertex in the graph.

Example:

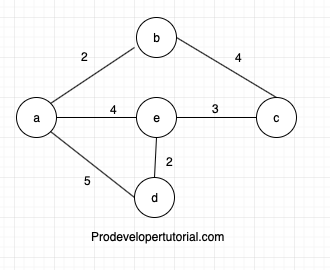
So to find the shortest path between “A” and “C”, you can reach from “A” to “C” by:

A -> E -> C =  4 + 3 = 7

A -> B -> C = 2 + 4 = 6

A -> D -> E -> C = 5 + 2 + 3 = 9

Hence the shortest path is A -> B -> C.

So to solve this, we can generate all the possible paths from the source vertex to every other vertex. Find the weight of all the paths, compare those weights and find min of all those weights. This can be optimized using  Dijkstra’s algorithm.

Dijkstra’s algorithm is a greedy algorithm.

1. The algorithm works on both directed and undirected graphs.

2. All the edges should have positive weight.

3. Graph should be connected.

Step 1: Select any vertex as starting vertex.

Step 2: Make the distance for all other vertices as INF

Step 3: From the starting vertex, visit all its adjacent/ neighbouring vertices and write their cost/value.

Step 4: Now that we have finished visiting all the adjacent vertices, we make the source vertex as visited.

Step 5: Choose another vertex, such that, the distance from source vertex is minimum.

Step 6: Now write down the cost for reaching its adjacent nodes form the starting node, such that the distance should be minimum.

Step 7: Repeat till all the nodes have been visited.

The process of choosing the length of the new path form source vertex to destination vertex is lesser than the current value, then update with the shortest value.

This process is called as Relaxation.

Consider the graph below:

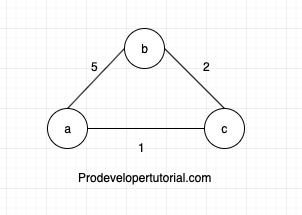
Now, what is the cost from “a” to “b”? It is 5.

But there is a path from “a” to “b” with less cost.

i.e “a” -> “c” -> “b”. the cost is 3.

Hence we will use this path from “a” to “b” through “c”. Because the cost is less. This is called as Relaxation.

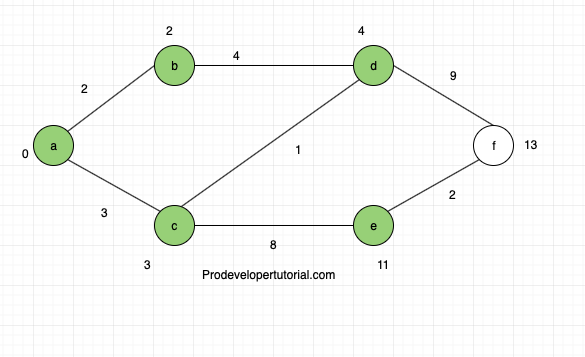
Consider the graph below:

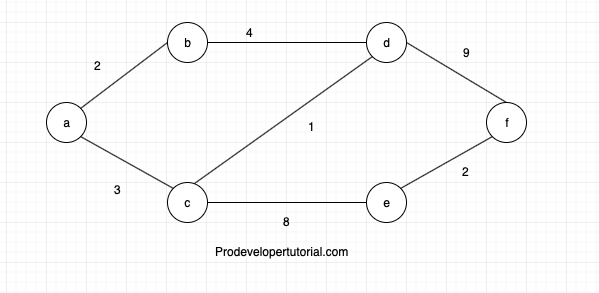
We shall select node “a” as starting node, we shall make all the nodes from node “a” to all other nodes as infinity and distance form “a” to “a” is zero.

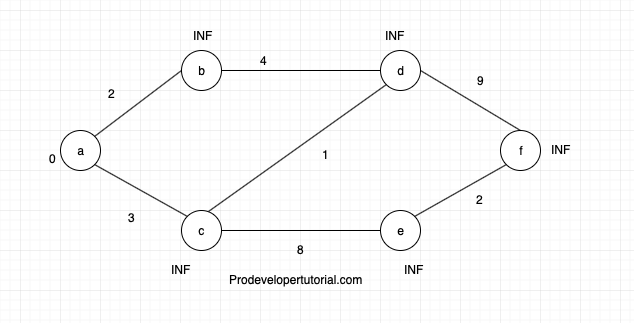
From node “a” check the adjacent nodes, i.e “b” and “c”, write down the cost in place of Infinity as they are less.

Now make node “a” as visited as all its adjacent nodes are visited.

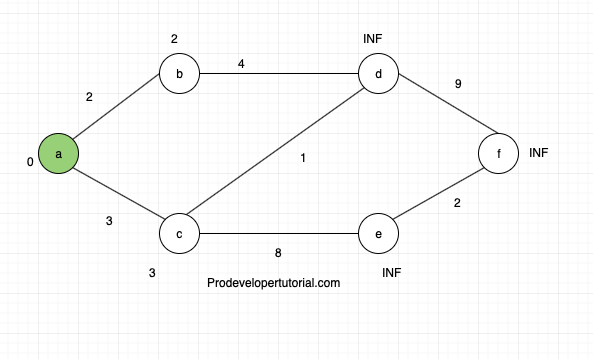
Now, check for the nodes that are of less cost.

Node “b” cost form “a” is 2.

Node “c” cost from “a” is 3.

Hence we shall choose node “b”.

Now we shall relax all the nodes adjacent to node “b”. Only node “d” is adjacent to node “b”. Hence total cost from “a” to “d” is

 a -> b + b -> d

 2 + 4 = 6

As 6 is less than INF, update the cost and make node “b” as visited.

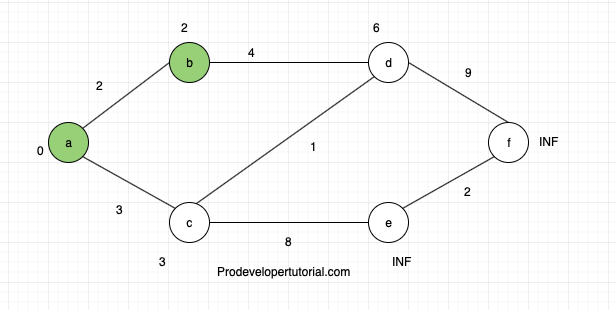
Now we choose node “c” as the cost is less when compared to node “d”.

Now try to relax all the nodes that are adjacent to node “c”. Node “d” and node “e” are adjacent.

Hence total cost at node “d” is:

 a -> c + c-> d

 3 + 1

 4

Total cost at node “e” is:

 a->c + c->e

 3+8

 11

Now make node “c” as visited.

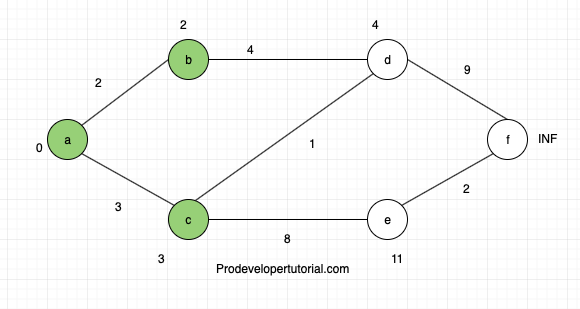
Now we choose node “d” as the cost is less than other 2 nodes.

Now relax all the edges adjacent to node d.

Node “c” and node “f” are adjacent.

Now total cost at node “c”:

 cost of node “d” + cost of “d” to “c”.

 4 + 1

 5

As “5” is greater than “3”. Don’t update the value.

Total cost of node “f”:

 cost of node “d” + cost of “d” to “f”

 4 + 9

 13

13 is less than INF. Hence update and mark it as visited.

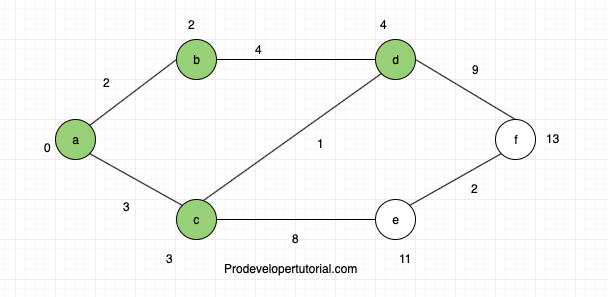
Now the cost is same for node “e” and node “f”. Choose any of the node.

We shall choose node “e”.

Node “e” and node “f” are adjacent.

Hence total cost of node “c”:

 cost of node “e” + cost of e -> c

 11 + 8

 19 > 3

 Hence don’t update.

Total cost of node “f”:

 Cost of node “e” + cost of e -> f

 11 + 2

 13

 Hence don’t update.

Make “e” as visited. Hence the solution

From the above steps we can use the below formula to calculate the code of the node.

Consider “u” as the source vertex.

“v” as the destination vertex.

Then if (distance(u) + cost of path (u, v) < distance_at (v))

   then

       distance(v) = distance_at(u) + cost of path (u, v)

#include <iostream>
#include <climits>

using namespace std;

const int numberVertex = 10;

int minDistance(int distance[], bool ShortestPathTree[])
{
    int min = INT_MAX, min_index;

    for(int vertex = 0; vertex < numberVertex; vertex++)
    {
        if(ShortestPathTree[vertex] == false && distance[vertex] <= min)
        {
            min = distance[vertex];
            min_index = vertex;
        }
    }

    return min_index;
}

void dijkstra(int graph[numberVertex][numberVertex], int source)
{
    int distance[numberVertex];
    bool ShortestPathTree[numberVertex];

    for(int i = 0; i < numberVertex; i++)
    {
        distance[i] = INT_MAX;
        ShortestPathTree[i] = false;
    }

    distance[source] = 0;

    for(int count = 0; count < numberVertex - 1; count++)
    {
        int u = minDistance(distance, ShortestPathTree);

        ShortestPathTree[u] = true;

        for(int vertex = 0; vertex < numberVertex; vertex++)
            if(ShortestPathTree[vertex] == 0 && graph[u][vertex] != 0 &&
                distance[u] != INT_MAX && distance[u] + graph[u][vertex] < distance[vertex])
                distance[vertex] = distance[u] + graph[u][vertex];
    }

    cout << "Distance from Source:" << endl;
    cout << "Vertex\t\tDistance" << endl;
    for(int i = 0; i < numberVertex; i++)
        cout << i << "\t\t" << distance[i] << endl;
}

int main()
{
    int graph[numberVertex][numberVertex] = {{0, 14, 0, 7, 0, 0, 0, 8, 0, 10},
                                             {14, 0, 8, 0, 0, 0, 0, 11, 0, 0},
                                             {0, 8, 0, 7, 0, 4, 0, 0, 2, 0},
                                             {7, 0, 7, 0, 9, 12, 0, 0, 0, 5},
                                             {0, 0, 0, 9, 0, 0, 0, 0, 0, 0},
                                             {0, 0, 4, 0, 0, 0, 2, 0, 0, 11},
                                             {0, 0, 0, 12, 0, 2, 0, 1, 6, 15},
                                             {8, 11, 0, 0, 0, 0, 1, 0, 7, 0},
                                             {0, 0, 2, 0, 0, 0, 6, 7, 0, 0},
                                             {10, 0, 0, 5, 0, 11, 15, 0, 0, 0}};

    dijkstra(graph, 0);

    return 0;
}