Finding shortest path algorithm tutorial 1. Introduction to Bellman–Ford algorithm

In this chapter we shall learn about below topics:

Bellman Ford algorithm us used to find shortest path from source to destination. It can be solved through Dynamic Programming approach.

A simple example can be thought as travelling from city A to city B. There are multiple routs, you need to find the route that is cost effective.

With the help of Bellman Ford algorithm, we can find the shortest path from one node/vertex to all other nodes/vertices.

1. Graph should be connected

2. Graph should be weighted

3. Graph should be directed

4. Graph can have negative weights

5. Graph cannot have a cycle with negative total weight

Dijkstra algorithm will not work for a graph for –ve weight. But Bellman ford algorithm will work for –ve weight.

The basic working of the algorithm is that we relax each edge for [number of vertices -1] times.

1. Choose the source vertex and make the weights of all the vertices as Infinity.

2. The cost of the source will be zero, because it won’t cost anything from source vertex to itself.

3. For each edge try to relax the edge for |v -1| times

4. Repeat step 3 till al the edges are released.

Relaxation is a concept where we try to find the optimal distance by continuously shorting the calculated distance between the vertices with the value that we already know.

Below is the formula to be used for relaxation:

if (distance_of(edge.from) + edge.cost < distance(edge.to))

then

distance(edge.to) = (distance_of(edge.from) + edge.cost

1. Note: Once you relax all the edges for (n-1) times, then if you relax for the nth time, the value should remain same. If it changes, then the solution is not possible, then probably the graph has a cycle with negative total weight.

Consider the graph below:

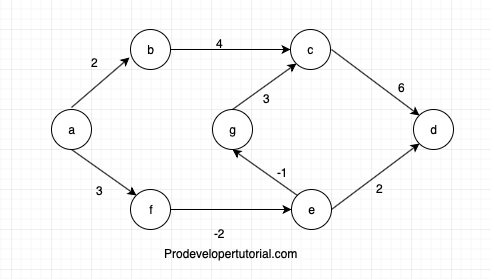
Consider “a” the initial nod, and make the distance from source “a” to all other vertices as infinity as shown in below image.

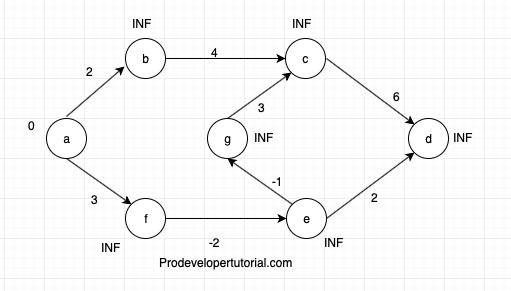
Now write down all the edges in the graph in any order.

[a, b], [a, f], [b, c] , [f, e] , [c, d] , [e, d] , [e, g] , [g, c]

Now we shall relax all the vertices [n-1] times.

Iteration 1:We shall use the relaxation formula here:

if (distance_of(edge.from) + edge.cost < distance(edge.to))
 
      then
 
         distance(edge.to) = (distance_of(edge.from) + edge.cost

[a, b]= distance_of(edge.from) = 0
 
                  edge.cost = 2
 
                  distance(edge.to) = INF
 
                 
 
0 + 2 < INF= TRUE. Now remove INF and insert 3 for b.

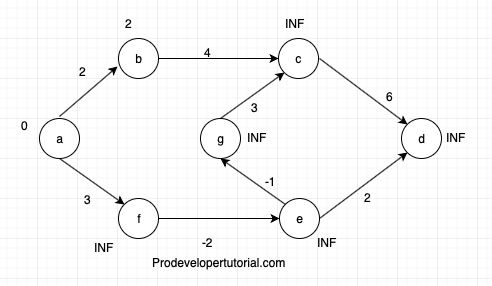
[a, f]= distance_of(edge.from) = 0
 
                  edge.cost = 3
 
                  distance(edge.to) = INF
 
                 
 
0 + 3 < INF= TRUE. Now remove INF and insert 3 for f.

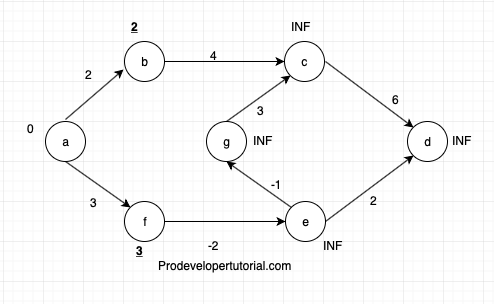
b, c]= distance_of(edge.from) = 2

                  edge.cost = 4

                  distance(edge.to) = INF

                 

2 + 4 < INF= TRUE. Now remove INF and insert 6 for c.

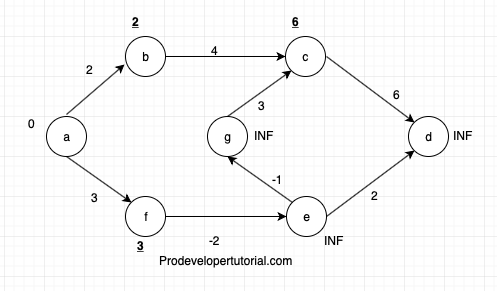
[f, e]= distance_of(edge.from) = 3

                  edge.cost = -2

                  distance(edge.to) = INF

                 

3 - 2 < INF= TRUE. Now remove INF and insert 1 for e.

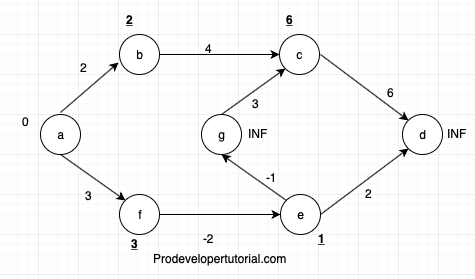
[c, d]= distance_of(edge.from) = 6

                  edge.cost = 6

                  distance(edge.to) = INF

                 

6 + 6 < INF= TRUE. Now remove INF and insert 12 for d.

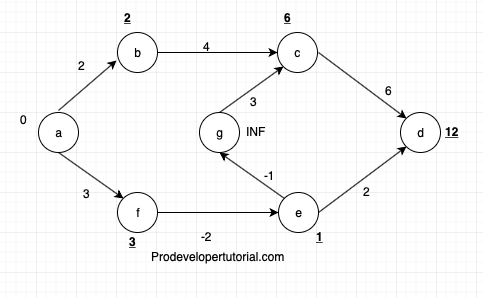
[e, d]= distance_of(edge.from) = 1

                  edge.cost = 2

                  distance(edge.to) = 12

                 

1 + 2 < 12= TRUE. Now remove INF and insert 3 for d.

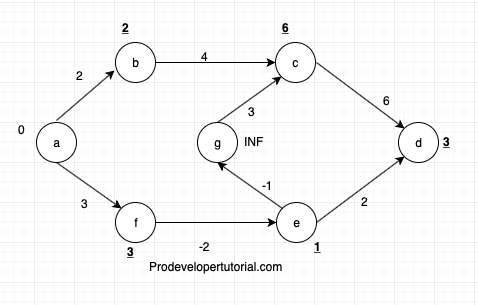
[e, g]= distance_of(edge.from) = 1

                  edge.cost = -1

                  distance(edge.to) = INF

                 

1 - 1 < INF= TRUE. Now remove INF and insert 0 for g.

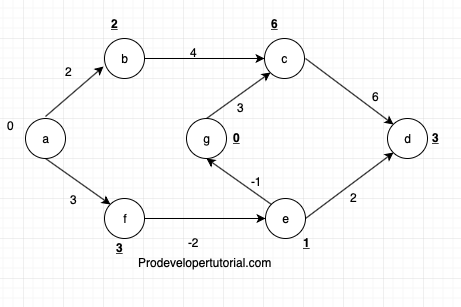
g, c]= distance_of(edge.from) = 0

                  edge.cost = 3

                  distance(edge.to) = 6

                 

0 + 3 < 6= TRUE. Now remove INF and insert 3 for c.

After the first iteration, the final distance is as shown below.

[a, b]      = 0 + 2 < 2,              b = 2

[a, f]        = 0 + 3 < 3,              f = 3

[b, c]      = 2 + 4 < 3,              c = 3

[f, e]       = 3 – 2 < 1,               e = 1

[c, d]      = 3 + 6 < 3,              d = 3

[e, d]      = 1 + 2 < 3,              d = 3

[e, g]      = 1 – 1 < 0,               g = 0

[g, c]       = 0 + 3 < 3,              c = 3

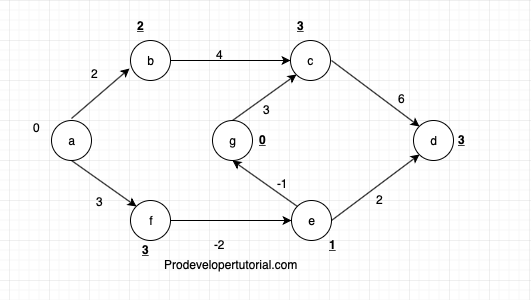
In the second iteration, there is no changes in the distance matrix. Hence we stop at second iteration.

After the second iteration, the final distance is as shown below:

#include <iostream>
using namespace std;

struct Edge
{
    int source, destination, weight;
};

struct Graph
{
    int V, E;
    struct Edge* edge;
};

struct Graph* createGraph(int V, int E)
{
    struct Graph* graph =
         (struct Graph*) malloc( sizeof(struct Graph) );
    graph->V = V;
    graph->E = E;

    graph->edge =
       (struct Edge*) malloc( graph->E * sizeof( struct Edge ) );

    return graph;
}
void printArr(int distance[], int n)
{
    cout<<"Vertex distance from Source"<<endl;
    for (int i = 0; i < n; ++i)
        cout<<i<<"   "<<distance[i]<<endl;
}

void BellmanFord(struct Graph* graph, int source)
{
    int V = graph->V;
    int E = graph->E;
    int distance[V];
    for (int i = 0; i < V; i++)
        distance[i]   = INT_MAX;
    distance[source] = 0;
    for (int i = 1; i <= V-1; i++)
    {
        for (int j = 0; j < E; j++)
        {
            int u = graph->edge[j].source;
            int v = graph->edge[j].destination;
            int weight = graph->edge[j].weight;
            if (distance[u] != INT_MAX && distance[u] + weight < distance[v])
                distance[v] = distance[u] + weight;
        }
    }
    for (int i = 0; i < E; i++)
    {
        int u = graph->edge[i].source;
        int v = graph->edge[i].destination;
        int weight = graph->edge[i].weight;
        if (distance[u] != INT_MAX && distance[u] + weight < distance[v])
            printf("Graph contains negative weight cycle");
    }

    printArr(distance, V);

    return;
}

int main()
{
    int V,E;
    cout<<"Enter no.of vertices and edges"<<endl;
    cin>>V>>E;
    struct Graph* graph = createGraph(V, E);

    int a[E][3];
    cout<<"enter source,destination and weight for each edge"<<endl;
    for(int i=0;i<E;i++)
    {
        cin>>a[i][0]>>a[i][1]>>a[i][2];
    }

    for(int i=0;i<E;i++)
    {
        graph->edge[i].source=a[i][0];
        graph->edge[i].destination=a[i][1];
        graph->edge[i].weight=a[i][2];
    }

	BellmanFord(graph, 0);

    return 0;
}