Sorting Algorithm 11: Counting Sort 

In this chapter we shall learn about below topics:

Counting sort algorithm is a linear sort algorithm. This algorithm is not based on comparing the elements but rather counting of the elements.

Usually we use this algorithm with other algorithm for example radix sort algorithm.

Below are the steps how the algorithm works:

Step 1: Find the minimum and maximum value from the array.

Step 2: Create a second array from the minimum value to maximum value.

Step 3: Increment the second array whenever we find a number from the first array.

Step 4: Once all the numbers will be written, take the sum [see in the pic below].

Step 5: Place the elements in the respective positions. You will get the sorted array.

Consider the below array, we shall sort this array using counting sort algorithm.

From the image above, we know that 4 is the smallest element and 15 is the largest element.

Now create one more array to hold the elements from index 4 to 15 and also counting array to hold the count as shown below:

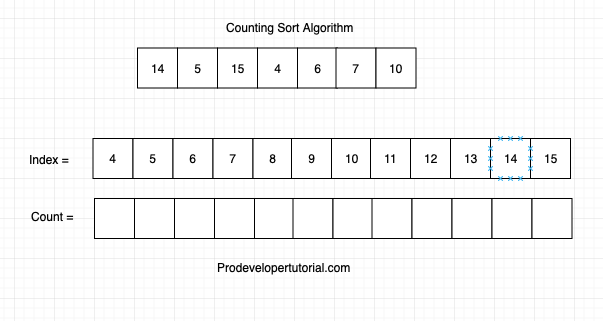
Now, count the number of times each element is repeated. Al the elements are repeated only once. Hence write 1 in their respective index as shown below;

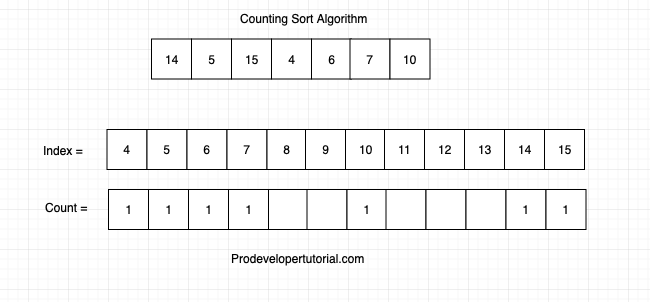
write 0, in all the index which are empty.

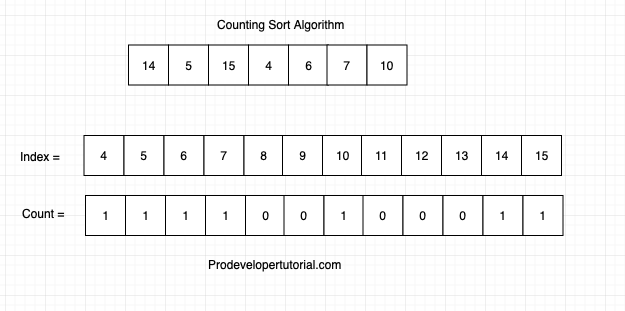
Now create a sum count array that will hold the sum of counts for the given index. Initially it will be as below:

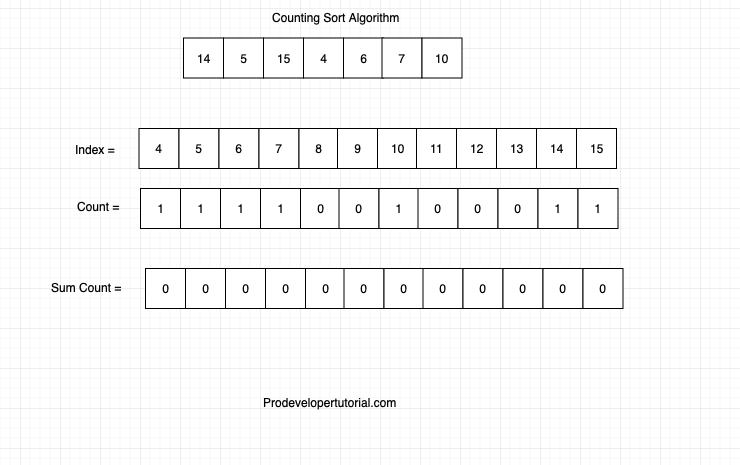
Now add the index and write down the sum count as shown below:

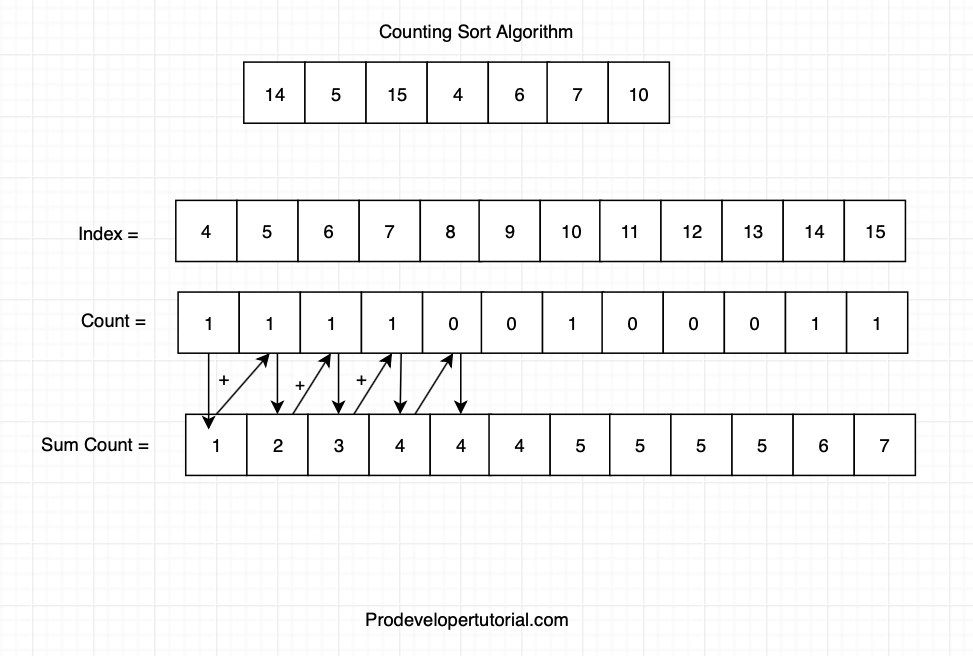
Now we shave filled out sum count array, let’s sort the input with the help of counting sort.

Create an output array. Initially the output array will be as below:

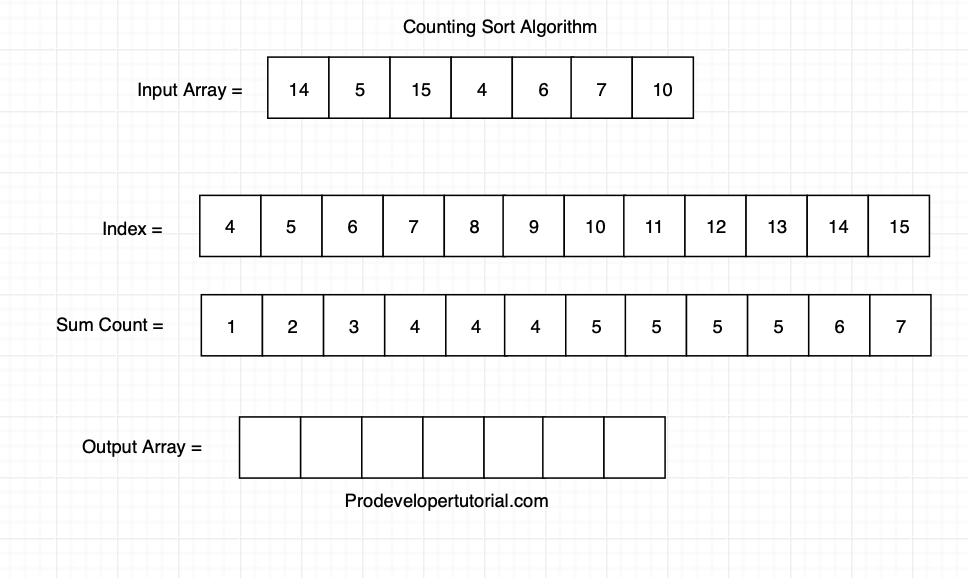
Now, check the element from input array and get the value from sumCount array and place it at its index.

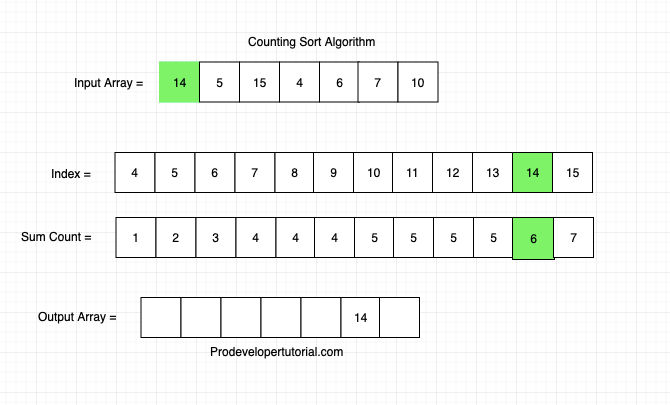
For example,

First element is 14.

The value for 14 in sumCount array is 6. Hence place 14 in index 6 in output array.

For 5, the value of 5 in sumCount array is 2. Hence place 5 in index 2.

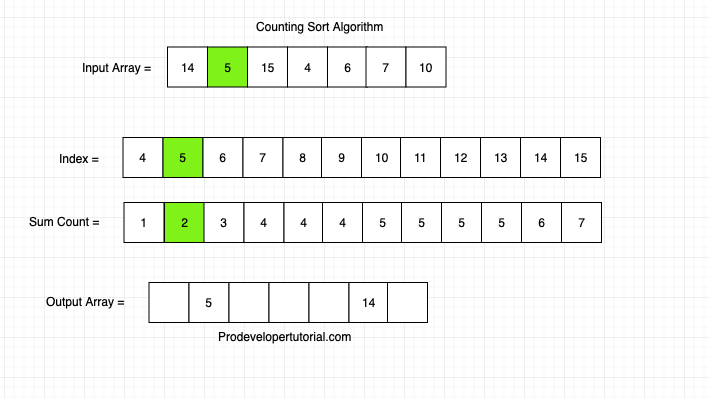
Similarly, do for all the elements we get sorted output as below:

#include<stdio.h>
#include<string.h>

void print_array(int array[], int length)
{
	int index = 0;

	printf("The sorted array is \n");

	for(index = 0 ; index < length ; index++)
	{
		printf("%d\n",array[index] );
	}
}


void counting_sort (int array[], int length)
{


	int max_number = array[0];
	int min_number = array[0];

	int i = 0;

	// find maximum and minimum number
	for ( i = 0; i < length; ++i)
	{
		if (array[i] > max_number)
			max_number = array[i];

		if (array[i] < min_number)
			min_number = array[i];
	}

    int range = max_number - min_number + 1;

	int counting_array [range];
	memset(counting_array, 0, sizeof(counting_array));


	// initialize the occurance of each element in counting array
	for ( i = 0; i < length; ++i)
	{
		counting_array[array[i] - min_number]++;
	}

	// calculate the sum of indexes
	int j = 0;
	for (int i = 1; i < range; i++)
	{
		counting_array[i] += counting_array[i - 1];
	}

	for (int i = 0; i < range; i++)
	{
		while( j < counting_array[i])
			array[j++] = i + min_number;
	}
	
}

int main()
{
	int length = 0;
	int array[100];
	int index = 0;

	printf("Enter the length of the array\n");
	scanf("%d", &length);

	printf("Enter the array elements of length %d\n", length);

	for (index = 0; index < length; ++index)
	{
		scanf("%d", &array[index]);
	}

	counting_sort(array, length);

	print_array(array, length);


}

Enter the length of the array
4
Enter the array elements of length 4
4
3
2
1
The sorted array is
1
2
3
4

Time complexity is O( n+r).