In the previous chapter we learnt about Big O notation, that defines tight upper bound. In this chapter we shall see about Big Omega and Big Theta notation.
6.1 Big Omega Ω:
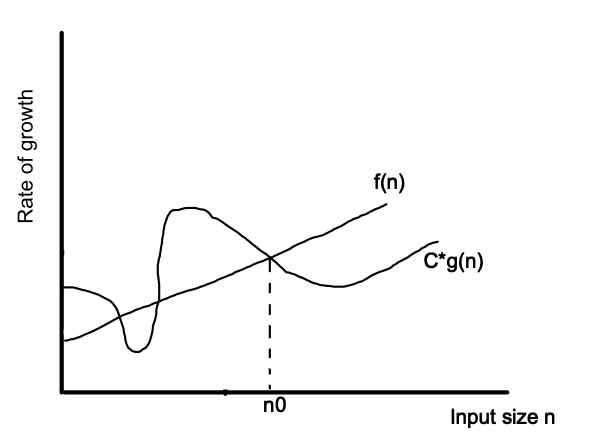
This notation is used to represent tight lower bound. Big omega can be defined as:
For a function f(n) is equal to Ω(g(n)) if there exist a constant C and n0 such that f(n) is always greater than C(g(n)). i.e. f(n) > C(g(n)) or C(g(n)) < f(n).
6.2 For example:
f(n) = 6 n^2 and Ω(n)
For C = 6 and n0 = 1, the function f(n) will always be greater than g(n).
Hence from the above example we can come to below image.
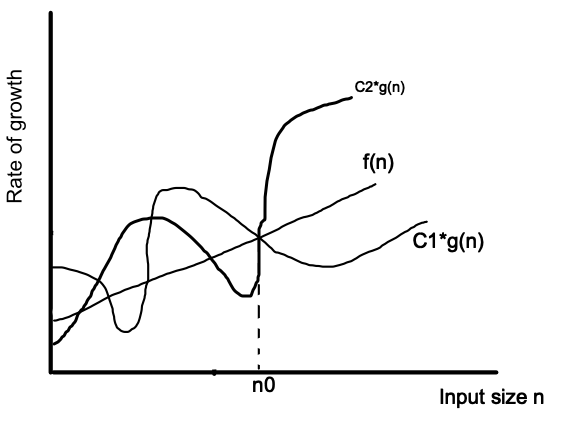
6.3 Big Theta Ø
Big theta is used to get the average case for a function. It can be defined as:
For a function f(n) is equal to Ø(n) if a function f(n) is greater than C1 g(n) and is less than C2g(n) for all n>= 0. i.e. 0<= C1 g(n) <= f(n) <= C2 g(n).