Problem Statement:
You are given a number “n”. You need to count the number of ways to construct the sum by throwing a dice one or more times.
Each throw produces a number between 1 and 6.
Example
n = 3
There are 4 ways to construct the sum:
1 + 1 + 1
1 + 2
2 + 1
3
Solution
We can solve this problem in number of ways.
1. Recursive
2. Top Down Approach
3. Bottom Up Approach
We shall study all the above methods.
1. Recursive
1. Create a recursive function that takes the sum “N” as input.
2. If you roll a dice, the numbers that are obtained are from 1 to 6.
3. Hence for every throw, subtract the dice value from the sum and call the recursive function again.
4. Along with that keep track of the count of number of ways that sum can be obtained.
Example:
If Sum = 3, the recursion tree will be:
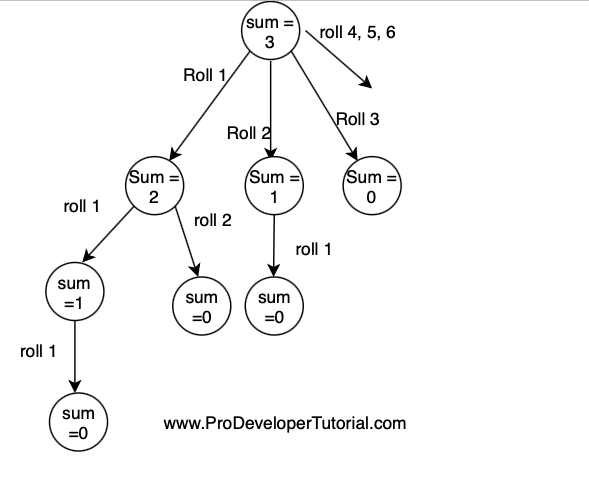
from the image above, we can see that, there are 4 different ways.
Every time you roll a dice, you remove that number from the sum and check again.
2. Top Down Approach
From the above image, we can see that there are overlapping sub problems.
FOr top down approach, we will use Memoization, it means, we will make use of a temp array to hold the intermediate values.
So we can do a top down DP approach, where we create a auxiliary/temp dp array with the size N+1 and initialize it to -1.
Then the base case would be if N == 0 then return 1.
Then while doing recursion, if any state dp[i] != -1, then we the value as it this substructure is already been calculated.
3. Bottom Up Approach
In the bottom up approach, we build the base case, then we move towards the target.
Here we will use tabular method. We take a table of size N+1;
The base case would be “dp[0] = 1”. It means, the number of ways that we get a sum = 0 is 1 times.
From there, we calculate the number of ways the sum can be made for, 1 to N.
i.e dp(i) will give the number of ways that the sum = i can be possible
Then at the end we will arrive at the solution at dp(n).
Now how to define dp(i) ?
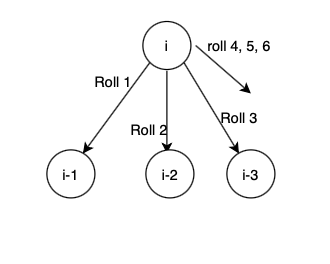
If we have a sum = i. Then the tree can be constructed as above.
From that we can derive the below formula
so dp(i) = dp(i-1) + dp(i-2) + dp(i-3)… + dp(i-6)
Solution in C++
#include <algorithm>
//visit www.ProDeveloperTutorial.com for 450+ solved questions
#include <iostream>
#include <string>
#include <queue>
#include <vector>
#include <unordered_set>
#include <list>
using namespace std;
int get_sum_count_recursion(int sum)
{
// base case
if (sum == 0)
{
return 1;
}
int count = 0;
// recursion for all the 6 states of a dice
for (int i = 1; i <= 6; i++)
{
// check if sum - i is greater than 0
// if true, increment the count
if (sum - i >= 0) {
count = count
+ get_sum_count_recursion(sum - i);
}
}
return count;
}
int get_sum_count_top_down_approach(int sum, int dp[])
{
// base Case
if (sum == 0) {
return 1;
}
// if the result is stored, then return it
if (dp[sum] != -1) {
return dp[sum];
}
int count = 0;
// Recur for all 6 states
for (int i = 1; i <= 6; i++)
{
if (sum - i >= 0) {
count = count
+ get_sum_count_top_down_approach(sum - i, dp);
}
}
return dp[sum] = count;
}
int get_sum_count_bottom_up_approach(int sum)
{
// Initialize dp array
int dp[sum + 1];
dp[0] = 1;
// iterate through intermediate values till sum
for (int i = 1; i <= sum; i++) {
dp[i] = 0;
//calculate sum for all the 6 states
for (int j = 1; j <= 6; j++) {
if (i - j >= 0) {
dp[i] = dp[i] + dp[i - j];
}
}
}
return dp[sum];
}
int main()
{
int sum = 3;
cout<<"Total number of ways using recursion "<<get_sum_count_recursion(sum)<<endl;
int dp[sum + 1];
memset(dp, -1, sizeof(dp));
cout<<"Total number of ways using top down approach "<<get_sum_count_top_down_approach(sum, dp)<<endl;
cout<<"Total number of ways using bottom up approach "<<get_sum_count_bottom_up_approach(sum)<<endl;
return 0;
}
Output:
Total number of ways using recursion 4
Total number of ways using top down approach 4
Total number of ways using bottom up approach 4