In this chapter we shall learn about below topics:
13.1 Introduction
13.2 Steps for performing Topological Sort
13.3 Implementation of Topological Sort in C++
13.4 Time complexity of Topological Sort
13.1 Introduction
Topological sort is used on Directed Acyclic Graph. Here the sorting is done such that for every edge u and v, for vertex u to v, u comes before vertex v in the ordering.
If the graph has a cycler if the graph us undirected graph, then topological sort cannot be applied.
Every DAG will have at least, one topological ordering.
13.2 Steps for performing Topological Sort
Consider the graph give below:
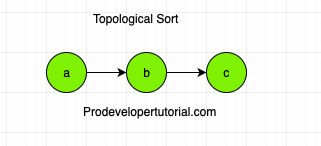
That graph is a directed and acyclic graph.
Hence according to the definition of topological sort, the order will be
a, b, c
Because “a” appears first, then “b”, then “c” in that order. Er shall see how to solve this by using khan’s algorithm.
Consider a DAG as below, we perform Topological Sort for that graph:
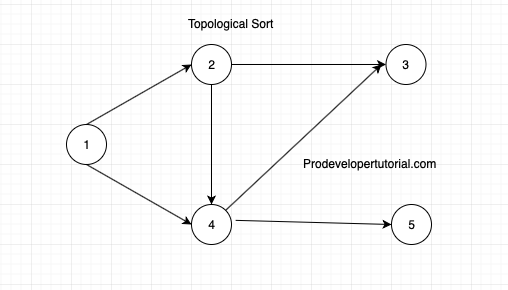
Step 1:
Find out the in degree of all the vertices. In degree means incoming nodes. Below image shows in degree of all the vertices.
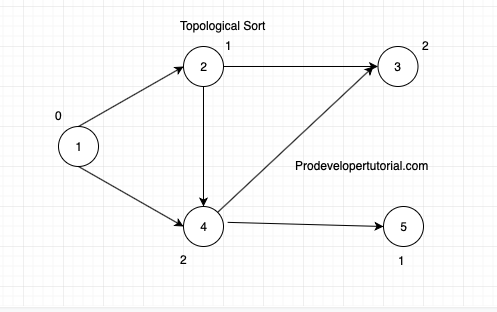
Step 2:
For the vertex with in degree 0, we start topological sorting from that node. We shave “1” node as in degree as 0. Now write “1” as output and delete that node and all the nodes that are outgoing from that node.
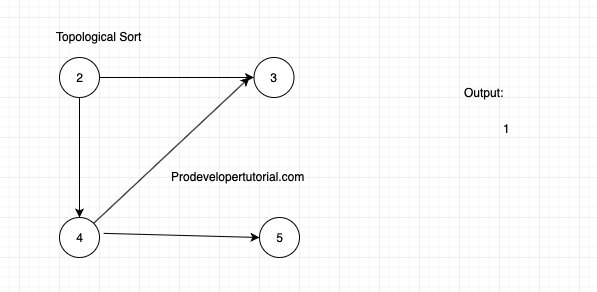
Now again calculate the in degree for all the vertices.
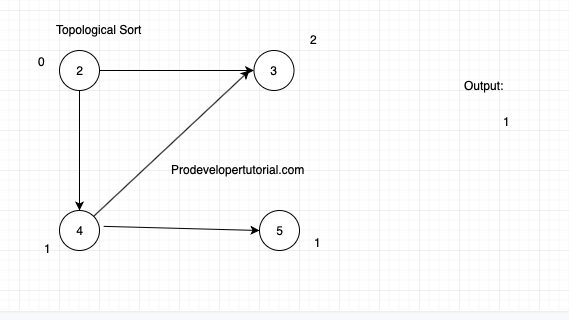
Again node “2” has in degree as 0. Take the node “2” and write in output. And delete all the outgoing vertex from node 2.
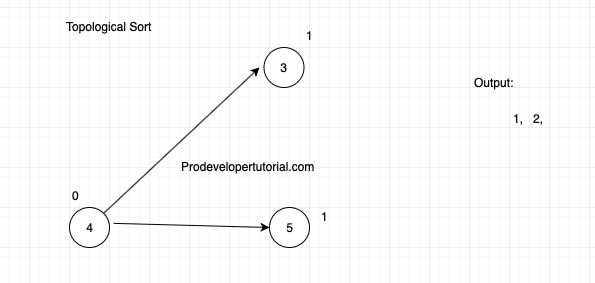
Again choose vertex with in degree 0, I.e node “4” and write in output and delete it’s outgoing edges.
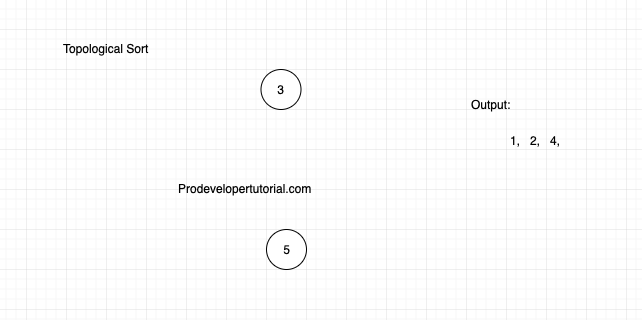
Now again calculate the in degree. From the above image, the in degree for both of the nodes are 0. Writ in any order as below:

This our result.
13.3 Implementation of Topological Sort in C++
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
vector<int> adj_list[100];
vector<int> topological_sort;
int in_degree[100];
int n; // number of vertices
int m; // number of edges
void perform_topsort()
{
queue<int>q;
for(int i=1;i<=n;i++)
{
//get the vertex with indegree 0 and push into the queue
if(in_degree[i]==0) q.push(i);
}
while(!q.empty())
{
int current_node = q.front();
q.pop();
topological_sort.push_back(current_node);
for(int i=0;i<adj_list[current_node].size();i++)
{
int v =adj_list[current_node][i];
in_degree[v]--;
if(in_degree[v]==0)
{
q.push(v);
}
}
}
}
int main()
{
cout<<"Enter the number of vertices[n], number of edges[m]"<<endl;
cin>> n>> m;
for(int i=0; i<=n; i++)
{
adj_list[i].clear();
}
topological_sort.clear();
memset(in_degree, 0, sizeof(in_degree));
cout<<"Enter the vertex in u->v fashion"<<endl;
for(int i=1; i<=m; i++)
{
int u, v;
cin>>u >>v;
adj_list[u].push_back(v);
in_degree[v]++;
}
perform_topsort();
if(topological_sort.size()!=n)
{
cout<<"Graph is not a DAG";
return 0;
}
cout<<"The topological sort is "<<endl;
for(int i=0; i<topological_sort.size(); i++)
{
cout<<topological_sort[i]<<"\n";
}
}
13.4 Time complexity of Topological Sort
Time complexity is O(V+E)