Unique Paths II in CPP

Problem Explanation:

A robot is located at the top-left corner of a m x n grid.
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid.
Now consider if some obstacles are added to the grids. How many unique paths would there be?

Example 1:

Input:
[
[0,0,0],
[0,1,0],
[0,0,0]
]
Output: 2

Explanation:

There is one obstacle in the middle of the 3×3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right

Before solving this solution, we have previously solved similar problem called “Unique Paths”. https://www.prodevelopertutorial.com/unique-paths-solution-in-c/

Similar to above problem, this problem can also be solved with the help of Dynamic Programming.

We understand the solution by taking an example below:

Consider the below 4 x 4 matrix as shown in image below:

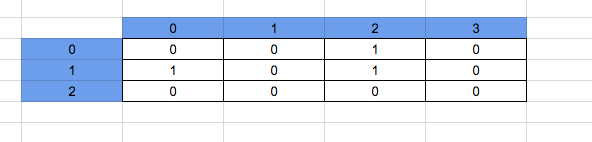
We solve by taking one grid at a time.

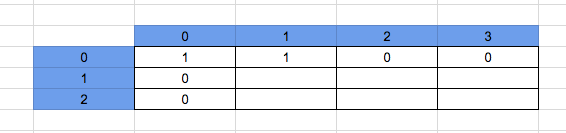
So the number of ways to arr[0][0] is 1.
The number of ways to arr[0][1] is 1, because we can arrive at this point by left side.
The number of ways to arr[0][2] is 0, because there is an obstacle.
The number of ways to arr[0][3] is also 0, because there is an obstacle at arr[0][2].

So the matrix will look as below:

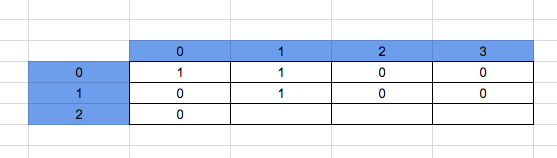
The number of ways to arr[1][0] is 0, because there is an obstacle.
The number of ways to arr[1][1] is 1, because there is a way from arr[0][1].
The number of ways to arr[1][2] is 0, because there is an obstacle.
The number of ways to arr[1][3] is 0, because there is an obstacle at arr[1][2].

Similarly, we solve the rest of the array, at the end we get the number of ways we can reach the end with obstacle.

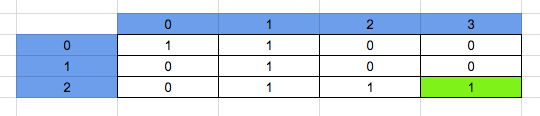
So form the above analysis we can conclude with the formula:
The number of paths at
arr[i][j] = arr [i – 1][j] + arr [i][j – 1] if input_array[i][j] != 1 and 0 otherwise.

Solution in C++

/*
* File     : unique_paths_II.cpp
* Author   : ajay.thousand@gmail.com
* Copyright: @ prodevelopertutorial.com
*/

#include<iostream>
#include<vector>

using namespace std;

#define m 3
#define n 4

int get_unique_paths_with_obstacle(int arr[m][n]) 
{
	int path [m] [n];

// Base condition
// initialize the array to 0
	for(int i=0;i<m;i++)
	{
		for(int j=0;j<n;j++)
		{
			path[i][j]=0;
		}
	}
// Base condition
	if(arr[0][0] == 1) return 0;    //no paths if the starting place is itself an obstacle
	path[0][0] = 1; //initializing the first position

// set the first row
	for(int i=1;i<m;i++)
	{ 
		if(arr[i][0]==0)
		{
			path[i][0] = path[i-1][0];
		}
	}

// set the first column
	for(int i=1;i<n;i++)
	{
		if(arr[0][i]==0)
		{
			path[0][i] = path[0][i-1];
		}
	}


// apply the formula path[i][j] = path [i - 1][j] + path [i][j - 1] if input_array[i][j] != 1 and 0 otherwise.

	for (int i = 1; i < m; i++)
		for (int j = 1; j < n; j++)
			if (!arr[i][j])
				path[i][j] = path[i - 1][j] + path[i][j - 1];

			return path[m - 1][n - 1];
}

int main()
{
	int arr [m][n];

	for (int i = 0; i < m; ++i)
	{
		for (int j = 0; j < n; ++j)
		{
			// inserting obstacle
			if ( (i == 0 && j == 2) || (i == 1 && j == 0)||(i == 1 && j == 2))
			{
				arr[i] [j] = 1;
				continue;
			}
			
			arr[i] [j] = 0;
		}
	}

	cout<<"Input array is "<<endl;
	for (int i = 0; i < m; ++i)
	{
		for (int j = 0; j < n; ++j)
		{
			cout<< arr[i][j]<<" ";
		}
		cout<<endl;
	}

	int result = get_unique_paths_with_obstacle(arr);

	cout<<"The number of unique paths for a "<<m <<" x "<< n<<" matrix is = "<< result<<endl;

	return 0;
}