Unique Binary Search Trees

Problem Statement:

You are given a number “n”.

You need to find out structurally unique binary trees that are possible.

Example

Input: n = 3
Output: 5

Solution

We can solve this problem with the help of DP

1. Top Down Approach

2. Bottom Up Approach

First we will see some examples:

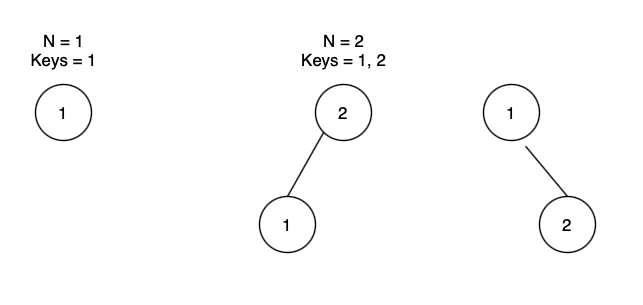
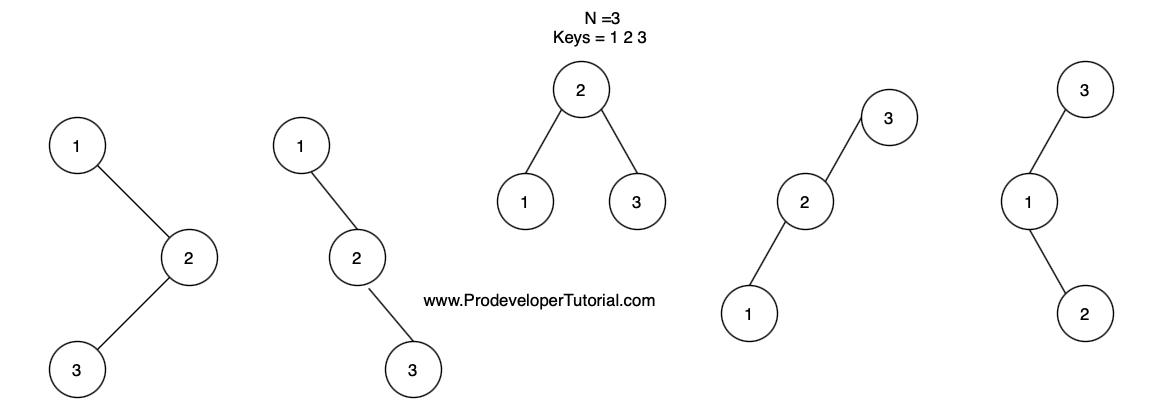
Below are the number of ways you can form a BST with n = 1, 2, 3

When N = 4, keys will be {1, 2, 3, 4}
Now we will compute total BST possible, by keeping “1” as root, “2” as root, “3” as root, “4” as root.

The trees will look like below:

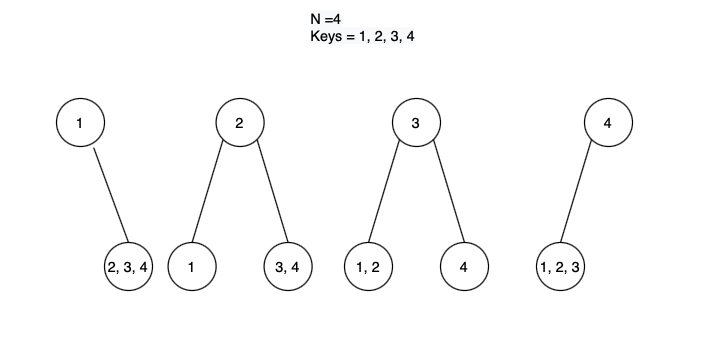
So from the above image, we can get the

total_no_of_bst(4) = total_no_of_bst_with_root_as (1) +
					 total_no_of_bst_with_root_as (2) +
 					 total_no_of_bst_with_root_as (3) +
					 total_no_of_bst_with_root_as (4) 

Now lets look at the RHS:

We will try to compute total number of combination possible if the root is “2”

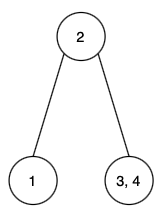
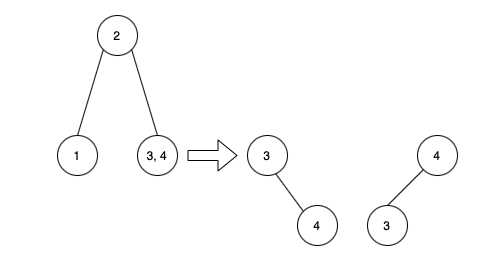
You can see that on the right node, there are 2 nodes “3, 4”. They are be arranged by keeping 3 as root, and by keeping 4 as root.

On the LHS side, there is only one node “1”. So there is only 1 way possible.

We can see that we can combine any one combination from LHS to any of the combination from RHS to form a unique BST with root as “2”.

i.e 1 * 2

It means, we have sub-divided the problem into smaller sub problems. i.e we are computing the value when N = 2 on the RHS side.

So we can convert total_no_of_bst_with_root_as (2) as numOfBst(1) * numOfBST(2);

Similarly

total_no_of_bst(4) = numOfBst (0) * numOfBst(3)+
					 numOfBst (1) * numOfBst(2)+
 					 numOfBst (2) * numOfBst(1)+
					 numOfBst (3) * numOfBst(0)

So dp[4] = dp[3] +
		   (dp[1] * dp[2]) +
		   (dp[2] * dp[1]) +
		    dp[3]

So dp[5] = dp[4] +
		   (dp[1] * dp[3]) +
		   (dp[2] * dp[2]) +
		   (dp[3] * dp[1]) +
		    dp[4]

We can arrive at generic pattern as:

(dp[0] * dp[n - 1]) + 
(dp[1] * dp[n - 2]) + 
(dp[2] * dp[n - 3]) + 
.... +  
(dp[n - 1] * dp[0])


So we can solve this by DP.

1. Recursion

2. Top down approach

3. Bottom Up approach

In the bottom up approach, we start from the base case and move towards the solution. i.e when N = 1, 2, 3, .. N

Solution in C++

#include <algorithm>  
#include <iostream>    
#include <string>
#include <queue>
#include <vector>
#include <unordered_set> 
#include <list> 

using namespace std;

vector<int> dp;

int get_ways_recursive(int n) 
{
    int result = 0;

    if(n==1 || n==0)
        return 1;

    for(int i=0;i<n;i++)
        result += get_ways_recursive(i)*get_ways_recursive(n-i-1);

    return result;
}

int util(int n, vector<int>& dp)
{
    if(dp[n] != 0)
    {
        return dp[n];
    }
    else
    {
        int ret=0;
        for(int i=0; i<n; i++)
        {
            ret += util(i, dp)*util(n-i-1, dp);
        }
        dp[n]=ret;
        return ret;
    }
}

int get_ways_top_down(int n) 
{
    vector<int> dp(n + 1, 0);

    dp[0] = dp[1] = 1;
    
    return util(n, dp);
}

int get_ways_bottom_up(int n) 
{
    
    if (n == 0 || n == 1)
        return 1;
    
    vector<int> dp(n+1);
    dp[0] = 1;
    dp[1] = 1;
    for (int i = 2; i < n+1; i++)
        for (int j = 0; j < i; j++)    
            dp[i] += (dp[j] * dp[i-j-1]);
    return dp[n];
}

int main(int argc, char const *argv[])
{
  cout<<"The number of ways for BST with N = 5 recursively is "<< get_ways_recursive(5)<<endl;
  cout<<"The number of ways for BST with N = 5 top down is "<< get_ways_top_down(5)<<endl;
  cout<<"The number of ways for BST with N = 5 bottom up is "<< get_ways_bottom_up(5)<<endl;

  return 0;
}

Output:

The number of ways for BST with N = 5 recursively is 42
The number of ways for BST with N = 5 top down is 42
The number of ways for BST with N = 5 bottom up is 42