Robbing Houses

Problem Statement:

You are given an array that represents the value present inside a house.

You need to rob the houses in such a way that no two adjacent houses should be robbed.

You need to return with max amount you can rob.

Example

Input arr = {2, 7, 9, 3, 1}
Output: 12

Start with house 1 (amt = 2), then rob house 3 (amt = 9) then rob house 5 (amt = 1).

Total sum of amount robbed will be 12

Solution

We can solve this by DP.

Before that we need to check if the problem satisfies 2 conditions of DP.

1. Optimal Solution
2. Overlapping Subproblem.

After that we need to get the recurrence relation, from there we can arrive at the solution.

First we will discuss the solution:

For every index/house the robber has 2 choices.

Choice 1: He can rob the house and he cannot rob the next house. Let the current house be i. Then he cannot rob (i+1) house. He can only rob (i+2) house.

sum = current_house_value + rob(i-2)

Choice 2: He will not rob the current house and can rob the next house. If the current house is “i”, then he can rob (i+1) house.

So if the i house is not selected, then rob(i+1)

So we can write the formula as:

If_ith_house_is_selected = current_house_value + rob(i+2)
If_ith_house_is_not_selected = rob(i+1)

Then we need to take the max of the above 2 values.

The recurrence tree can be as below for f(n).

At every index, we can either choose to rob the house and goto i+2 house or we dont need to rob and go to i+1 house.

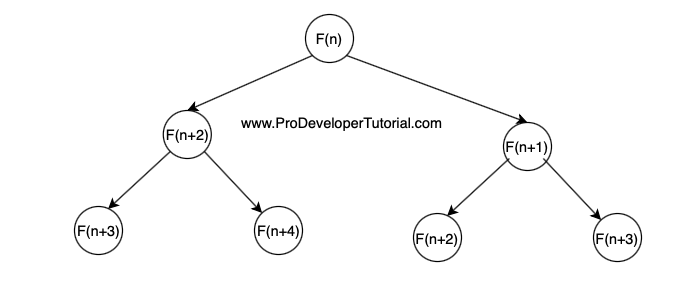
From the above image, we can see that the problem satisfy both of the DP conditions.

Hence we can solve it by using

1. Recursion
2. Top Down
3. Bottom Up

Basic understanding:

1. If i = 0, then the max value is arr[0]
2. If i = 1, then the max value is max(arr[0], arr[1])
3. If i = 2, then the max value will depend on if we have chosen the previous value or not.

Solution in C++

#include <algorithm>  
#include <iostream>    
#include <string>
#include <queue>
#include <vector>
#include <unordered_set> 
#include <list> 

using namespace std;

vector<int> dp;

int recursive_util(vector<int>& nums, int index)
{
    if(index>=nums.size())
      return 0;
    
    return max(nums[index]+recursive_util(nums,index+2),recursive_util(nums,index+1));
}

int get_max_amount_recursive(vector<int>& nums) 
{
    return recursive_util(nums,0);
}

int top_down_util(vector<int>& nums, int index, vector<int> &dp)
{
  if( index >= nums.size())
    return 0;

  if(dp[index]!=-1)
    return dp[index];

  return dp[index] = max(nums[index]+top_down_util(nums,index+2,dp),top_down_util(nums,index+1,dp));
      
}

int get_max_amount_top_down(vector<int>& nums) 
{

  vector<int>dp(nums.size()+1,-1);
  return top_down_util(nums, 0, dp);
}

int get_max_amount_bottom_up(vector<int>& nums) 
{
  vector<int> dp(nums.size(), -1);
  dp[0] = nums[0], dp[1] = max(nums[0], nums[1]);

  for (int i=2; i<nums.size(); i++)
    dp[i] = max(dp[i-1], nums[i]+dp[i-2]);

  return dp[nums.size()-1];
}

int main(int argc, char const *argv[])
{
  vector<int> nums = {2, 7, 9, 3, 1};
  cout<<"The max amount to rob recursively is "<< get_max_amount_recursive(nums)<<endl;
  cout<<"The max amount to rob top down is "<< get_max_amount_top_down(nums)<<endl;
  cout<<"The max amount to rob bottom up is "<< get_max_amount_bottom_up(nums)<<endl;

  return 0;
}

Output:

The max amount to rob recursively is 12
The max amount to rob top down is 12
The max amount to rob bottom up is 12