Longest Palindromic Substring In C++

There are 3 approaches, in this topic we shall discuss 2 methods

1. Brute force approach. Time Complexity O(n ^ 3)

2. Dynamic Programming. Time Complexity O(n ^ 2)m space complexity O(n ^ 2)

3. Manacher’s algorithm, discussed in separate post.

Time complexity: O(n^3)

In this approach, we take all possible substring in the given string and then take their reverse. And we shall match the reverse with the given substring. Hence checking the longest substring.

Input String “aba”

Possible Substring Reverse of substring

a a
ab ba
aba aba
ba ba
b b
a a

Hence the output will be “aba” as it is the longest palindromic substring.

For this approach, we take 2 loop, outer for loop, and inner for loop.

Then call the “check_palindrome” function to display the longest palindrome.

#include<iostream>
#include<string>
using namespace std;

bool isPalindrome(string str)
{
    if (str.length() == 0)
        return false;

    if (str.length() == 1)
        return true;

    int halflen = str.length() / 2;
    int len = str.length() - 1;

    for (int i = 0; i < halflen; i++)
    {
        if (str[i] != str[len])
        {
            return false;
        }
        len--;
    }
    return true;
}

string bruteForceGetLongestPalindrome(string input_str)
{
    int palindromeLength = 0;
    string resultstring = "";

    //loop to get substring 

    for (int i = 0; i < input_str.length(); ++i)
    {
        string subString = "";
        subString += input_str[i];

        for (int j = i + 1 ; j < input_str.length(); j++)
        {
            subString += input_str[j];

            //check if the substring is a palindrome
            if( isPalindrome (subString) ) 
            {
                if (palindromeLength < subString.length())
                {
                    palindromeLength = subString.length();
                    resultstring += subString;
                }
            }

        }

    }
    return resultstring;
}

int main()
{
    string resultstring = bruteForceGetLongestPalindrome("ashdkabajjseiw");
    cout<<"The longest substrinng is " << resultstring <<endl;

}

Dynamic programming is dividing a complex problem into smaller sub problems and solving those sub problems and storing the result of those sub problems in the memory like a table or an array and comeback to check those results when ever needed.

In our solution approach we use 2D Boolean array to store the results.

Let us take an example

“abaab” is the string, we need to get the longest palindromic substring.

In pass 1, length =1 here i = j
Hence substring of [0][0], [1][1], [2][2], [3][3], [4][4] are true. As shown in figure 1.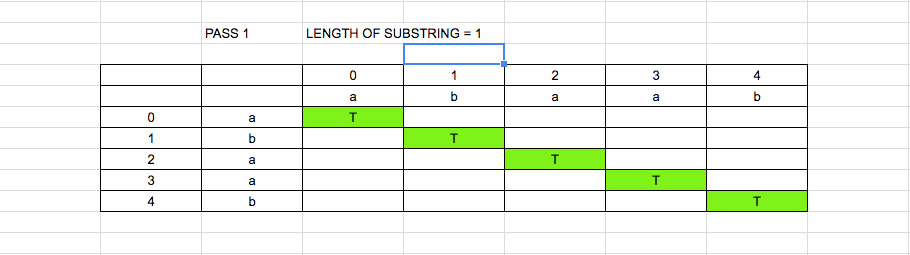

In pass 2, length = 2 here j = i+1
Hence the truth value of the substrings [0][1], [1][2], [2][3], [3][4] are updated if both the values are same. As shown in figure 2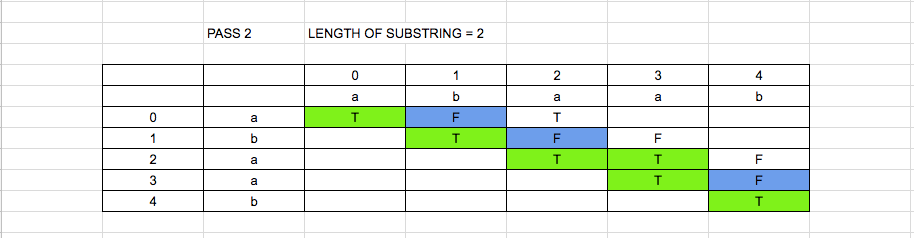

For a string to be considered as a palindrome, we use the below formula:

If (str [i] == str[j] and table_value [i +1] and [j -1] is true) then the string is a palindrome.

In the pass 3 we get to know how the above formula works:

In pass 3, length = 3 here j = i + 2
Hence we look at the substrings [0] [2], [1] [3], [2] [4]. As we can see from the table below, “aba” is a palindromic substring we have got.

For a string to be palindrome we need to check if the first and last character are same. Because the middle character value has already been calculated and stored in the array.

In pass 4, length 4 here j = I + 3
Hence the substrings will be [0][3], [1][4].

Here we get the substring “baab”, here have to calculate the value of [1] [4], all other values have already been filled. Hence the solution.

Here the time complexity is O (n ^2)

Space complexity is also O(n ^2)

#include<iostream>
#include<string>
using namespace std;

string DynamicProgrammingGetLongestPalindrome(string input_str)
{
    if(input_str.length()<=1)
        return input_str;
    int string_length = input_str.length();
    int palindromeLength = 0;
    bool bArray[string_length] [string_length];

    string resultstring = "";

    for (int current_length = 0; current_length < string_length; current_length++)
    {
        for (int i = 0; i < string_length -1 ; i++)
        {
            int j = i + current_length;

                if(input_str[i]==input_str[j] && (j-i<=2 || bArray[i+1][j-1]))
                {
                    bArray[i][j]=true;
 
                    if(j-i+1>palindromeLength)
                    {
                       palindromeLength = j-i+1; 
                       resultstring = input_str.substr(i, j+1);
                    }
            }
        }
    }
    return resultstring;


}


int main()
{
    string resultstring = DynamicProgrammingGetLongestPalindrome("xaabbaa");
    cout<<"The longest substrinng is " << resultstring <<endl;

}