From the above program we shall understand how stack frame gets effected when using recursion function.
So we called the function with n = 3 value. We know that, in C, local c variables are stored in stack. When you call a function, it’s activation record along with unction parameters are also stored.
So from main() function we call fun() function.
Stack Frame:
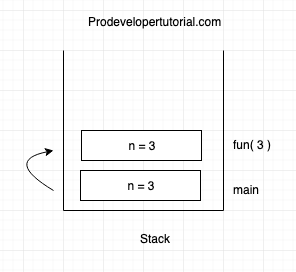
Changes in the fun() function:
int fun(3 )
{
if (n == 1)
return 1; // base case
else
return 1 + fun(2);
}
As we are calling fun (2), we transfer the control from fun (3) to fun (2) as shown above.
Now int fun (2)
Stack Frame:
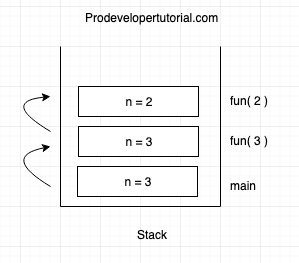
Changes in the fun() function:
int fun( 2 )
{
if (n == 1)
return 1; // base case
else
return 1 + fun(1);
}
Now we call fun (1) from fun (2). Hence we transfer the control from fun (2) to fun (1).
Stack frame:
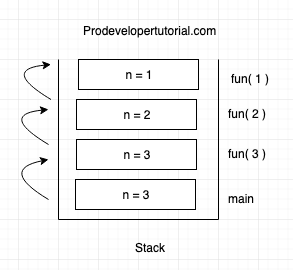
Changes in the fun () function.
int fun( 1 )
{
if (n == 1)
return 1; // base case
}
Now in fun (1) now “n == 1” is true, hence we return 1. Which mean, we are returning 1 to the calling function from the stack frame. We can see that the calling function is fun (2).
int fun( 2 )
{
else
return 1 + fun(1);
}
int fun( 2 )
{
else
return 1 + 1; // return 2
}
Hence, 2 will get returned to the calling function of fun (2).
From the stack frame, we can see that fun (3) is calling fun (2). Hence the fun (3) will become:
int fun( 3 )
{
else
return 1 + fun( 2 );
}
int fun( 3 )
{
else
return 1 + 2; // return 3
}
Now the value “3” will be returned to its calling function i.e main function.
On a high level we can summarize the above steps as below:

2.4 What is a Recursion Tree?
As we saw in previous section, we saw what a recursion is and how the stack frame changes when a recursive call is made.
A recursion tree is nothing but a visual representation of recursive calls.
Let’s understand the recursion tree by taking an example of printing n^th Fibonacci number.
The pseudo code to find nth Fibonacci number is as below:
fib( n )
{
int n <= 1
return n;
else
return fib ( n -1 ) + fib ( n - 2 )
}
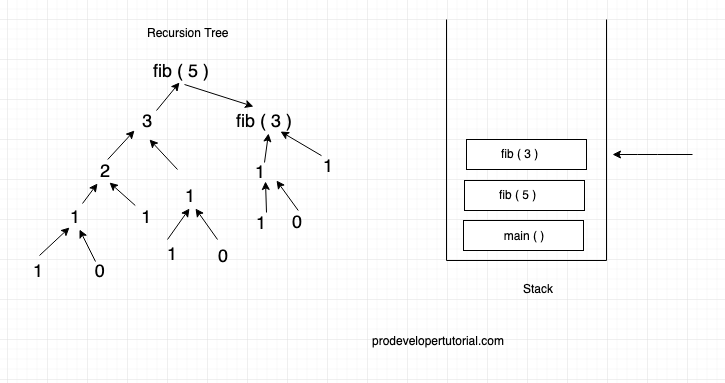
and when we call the fib function with n = 5. The stack framer and Fibonacci tree is as shown below:
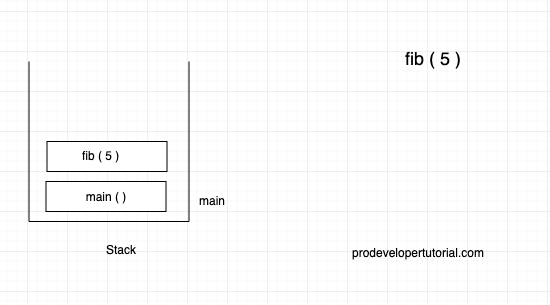
Then fib ( 5 ) is a recursive call it will be:
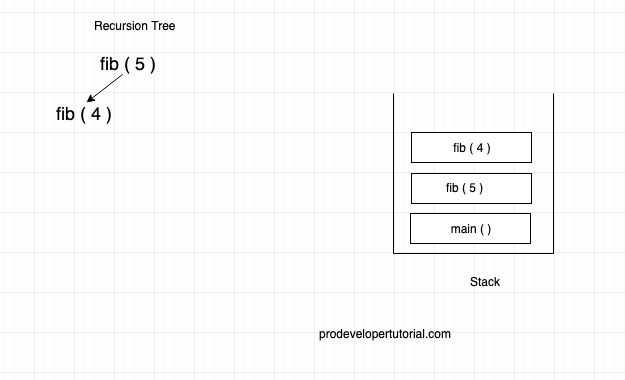
Right now the compiler is executing fib ( 4 ) all the other are in paused state.
Then fib ( 4 ) will make a call to fib ( 3 ), fib ( 3 ) will make a call to fib ( 2 ), fib (2) will call fib ( 1 )… it can be showed as below
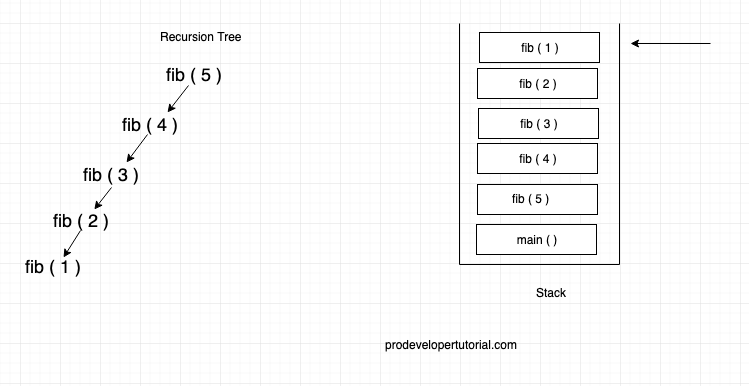
Now fib ( 1 ), it will return 1 and also it is popped from stack.
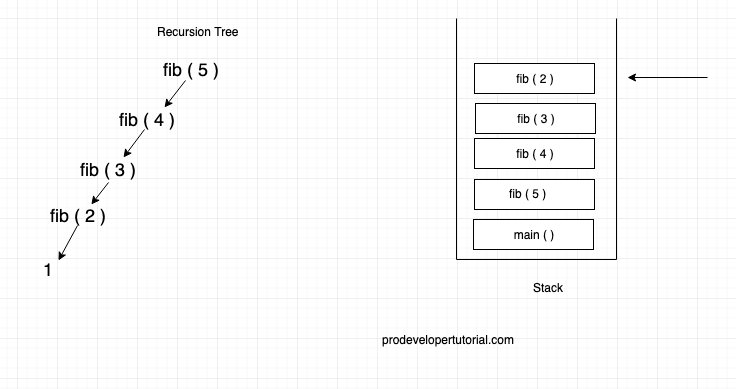
Now fib ( 2 ) is in stack, it will call fib ( 0 ) and fib (0) will be put into stack.
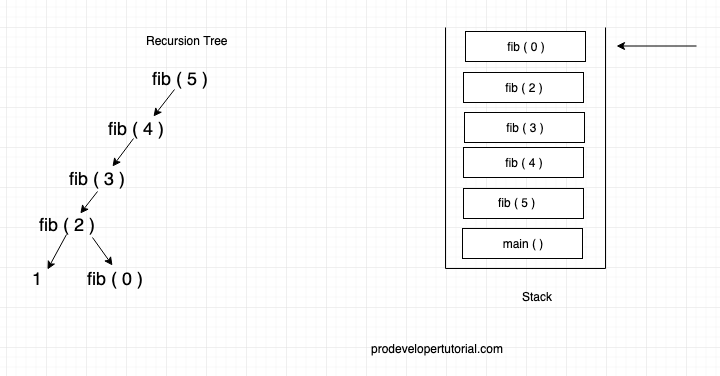
Now fib ( 0 ) will return 0 and as fib ( 2 ) has called fib ( 0 ) and fib ( 1 ) the final value for fib ( 2 ) will be 1, and fib ( 2 ) will be popped out of stack. Now the execution will flow to fib ( 3 ).
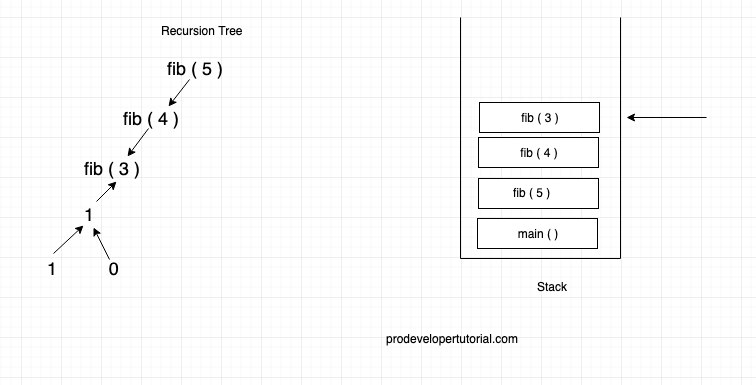
Now fib ( 3 ) already called fib ( 2 ) hence it will call fib ( 1 ) and fib ( 1 ) will be placed into the stack.
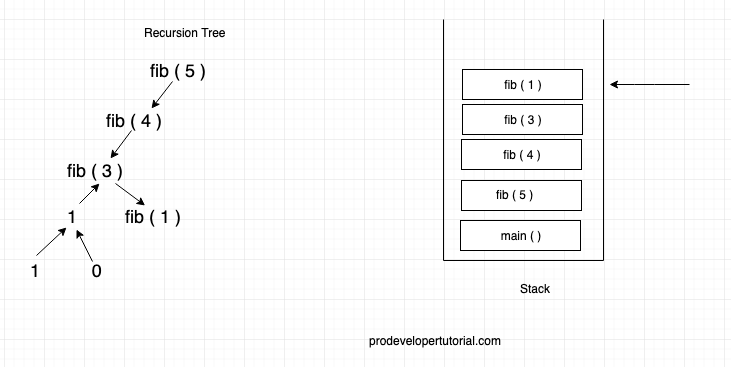
Again fib ( 1 ) will call fib ( 0 ) and it can be showed as below:
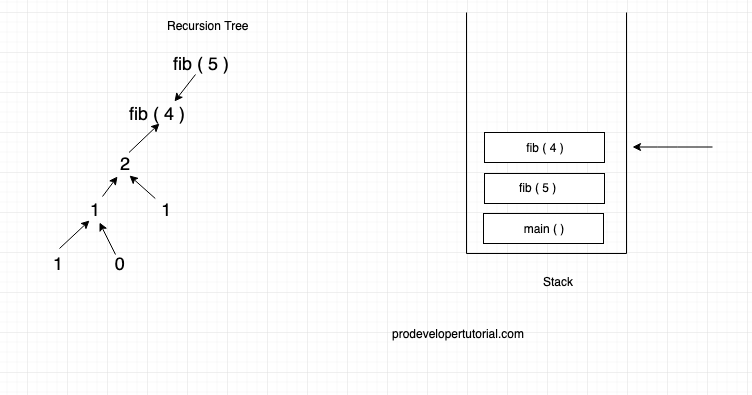
Now for fib ( 4 ), it already called fib ( 3 ), hence it will call fib ( 2 ), again fib ( 2 )will call fib ( 0 ) and fib ( 1 ).
The calculated values can be as below:
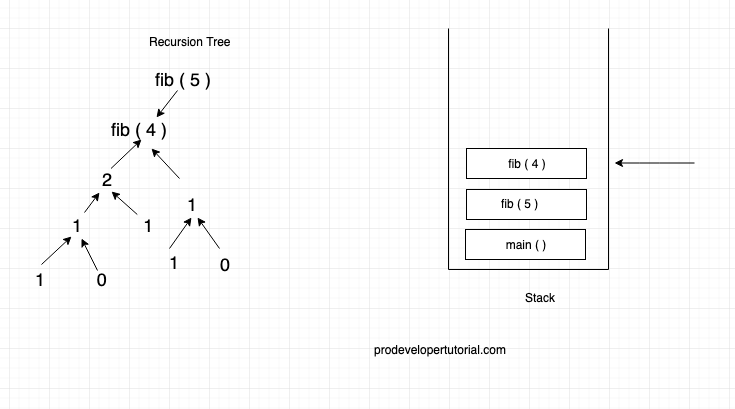
Hence fib ( 4 ) value will be “ 2 + 1 = 3”. 3 will be returned to fib ( 5 )
Again fib ( 5 ) will call fib ( 3 ), fib ( 3 ) will call fib ( 2 ), then fib ( 2 ) will call fib ( 1 ). Fib ( 1 ) will return 0.
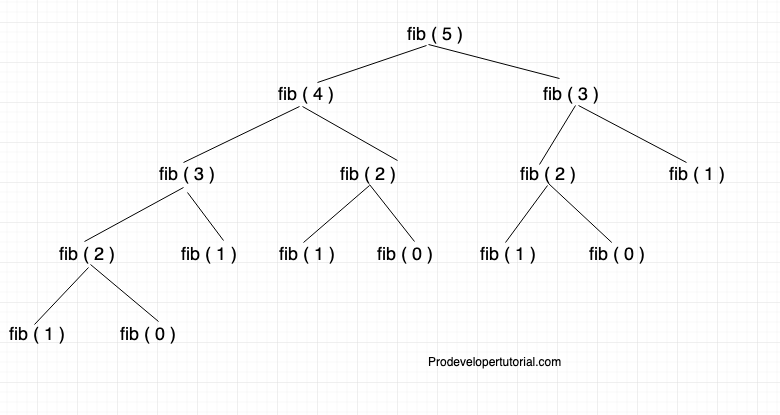
The final recursion tree will be as below:
This is the basic of recursion and the changes in the stack frame when you call a recursion function.
This is an important topic. Because in the next chapter i.e dynamic programming and backtracking it uses recursion to get the results.