Height or Max depth if a BTree

In this chapter we shall calculate the height of a Binary Tree.

Problem Statement:

Given the root node of binary tree, calculate the height of that tree.

Example:

Consider the tree below:

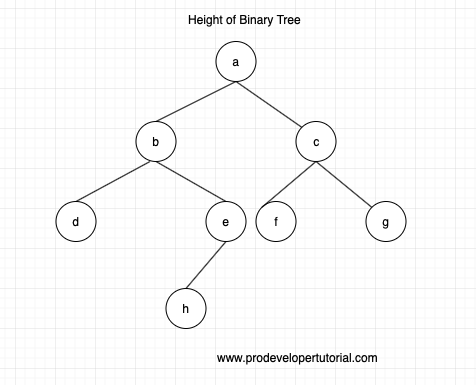
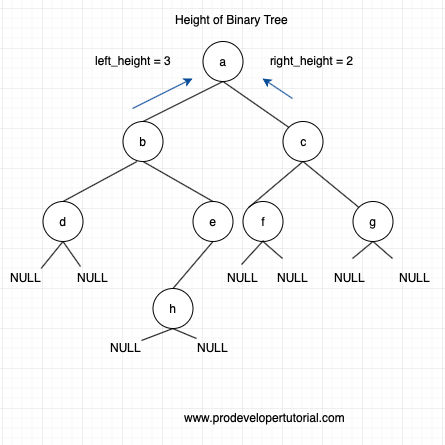
The height of the binary tree will be 4. The path will be:

a -> b -> e -> h

First we shall see how to calculate manually, after that we shall see how to calculate using recursion function programmatically.

So we know that:

Height of a node = 1 + number of edges on the longest path from the root to leaf.

So with help of this example we shall calculate the height of the tree.

To calculate the height of the tree, we need to calculate the number of edges from the leaf node.

In our example, we have d, h, f, g as leaves.

for d, there are 2 edges
for h, there are 3 edges
for f, there are 2 edges
for g, there are 2 edges

Now, the node has more number of edges is:

a -> b -> e -> h

Has the longest path.

Hence the height of the BTree is 1 + longest path.

i.e 1 + 3 = 4

Now let’s see how to calculate using recursion function:

The pseudo code is as below:

int get_height(root)
{
	if p == null, 
		return 0

	left_height = get_height(root -> left)
	right_height = get_height(root -> right)

	if left > height
		height = 1 + left
	else
		height = 1 + right

	return height

}

So above function we are basically performing 3 steps:

Step 1: Calculate the left height of all nodes recursively
Step 2: Calculate the right height of all nodes recursively
Step 3: Return the max of left and right height + 1

So with help of diagram, we shall see how this recursion function perform

We shall modify the diagram little bit to include null nodes also for the leaf nodes

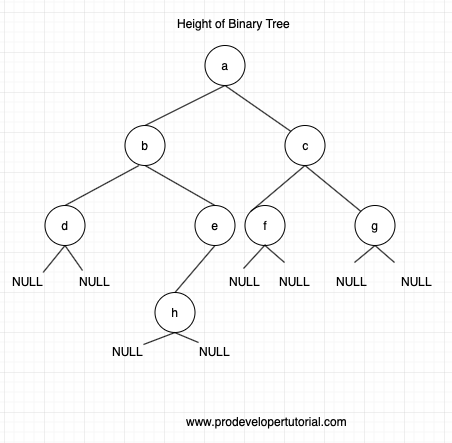
So when we are giving root node, as the first step is to go to its left node recursively.
We traverse all the left node of the root node till we reach NULL as shown below:

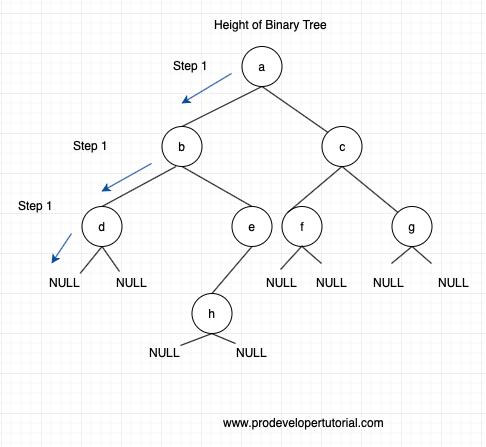
As you can see above, we traversed the left odes from the root node till we reach a null node.

When we reach the null node, we go one level up i.e to node “d” then traverse the right node to node “d”. Ass there is no right node to node “d”, we return 0.
This can be shown as below:

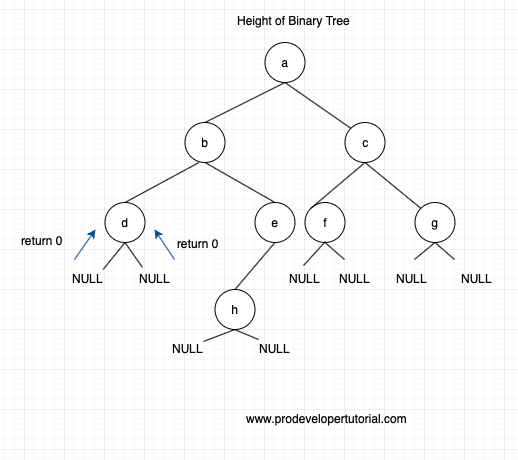
Now according to our return statement, we calculate the

max_of(left_value, right_value) + 1

For us, left value and right value is 0. Hence 0 + 1 = 1.
Hence height at node d is 1.

We return the value 1 to node b. Hence for node “b” the value for its left side has returned 1.

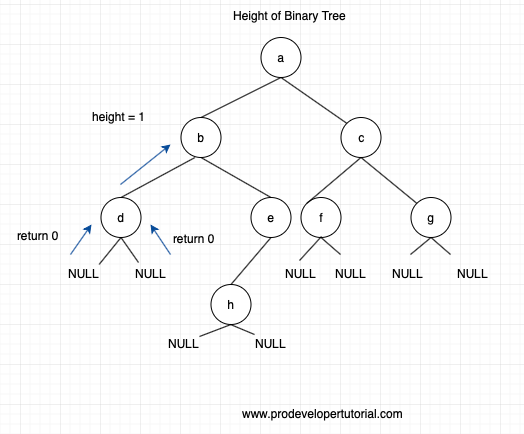
Now at node b, it will traverse towards right. Then it will reach node e. For node a, there is no right node, it will return 0.

For node e, there is left node. Hence it will go to node h.

For node h, there is no left and right node. Hence it is similar to node “d”, that we solved earlier. Hence the height at node h will be 1.

Similarly, the height at node “e” will be 2.

Now when we reach to node “b”, it has height = 1 from left node and height = 2 from right side as shown below

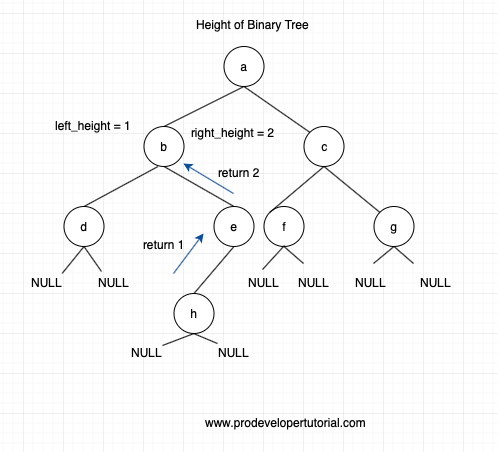
Now at ode b, we need to select max and add 1 to it and send it to node “a”.
Hence we shall select 2 + 1 = 3 and return 3 to node “a”.

Hence we shall select 2 + 1 = 3 and return to node “a”. This will be the total left height for node “a”.
Similarly, we calculate the right height for node “a”. It will be equal to “2”.

Again we need to select max of (3, 2) + 1

i.e 3 + 1 = 4. Hence the result