Given an directed graph, find the in and out degree of all vertices

Problem Statement:

You are given an directed graph, you need to find out the in and out degree of all the vertiecs.

Example

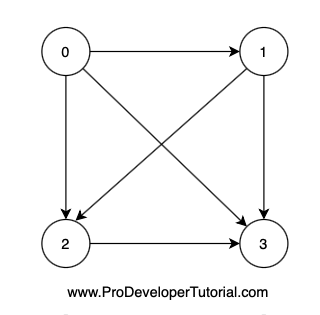
Vertex    In    Out
0          0    3
1          1    2
2          2    1
3          3    0

Solution

Solution is very simple.

We need to traverse the adjacency list for all the vertices.

The size of the adjacency list for each vertex is the size of out degree.

And increment the indegree of every vertex that has an incoming edge from a particular vertex.

Solution in C++

#include <algorithm>  
//visit www.ProDeveloperTutorial.com for 450+ solved questions  
#include <iostream>    
#include <string>
#include <queue>
#include <vector>
#include <stack> 
#include <list> 

using namespace std;

class Graph
{

private:
   int V; 
   list<int> *adj; // to hold adjacency list
 public:
   Graph(int V); // Constructor
   void add_edge(int v, int w); // to add an edge to graph
   void print_graph();
   void count_in_out_degree();
};

Graph::Graph(int V)
{
   // get the total number of nodes
   this->V = V;

   // initialize adjacency list for that number of nodes
   adj = new list<int>[V];
}

void Graph::add_edge(int v, int w)
{
   // add the edge to adjacency list
   adj[v].push_back(w); 
   // uncomment below to make the graph as undirected
   //adj[w].push_back(v); 
}

void Graph::print_graph()
{
   for(auto i = 0; i < V; i++)
   {
      cout<<"\nAdjacency list of vertex "<<i<<endl;

      for(auto j = adj[i].begin(); j != adj[i].end(); j++)
      {
         cout<<" ->"<<*j;
      }
   }
}

void Graph::count_in_out_degree()
{
     
    int *in_degree = new int[V];
    int *out_degree = new int[V];

   for(auto i = 0; i < V; i++)
   {
      out_degree[i] = adj[i].size();

      for(auto j = adj[i].begin(); j != adj[i].end(); j++)
      {
         int node = *j;
         in_degree[node]++;
      }
   }

    cout << "Vertex\t\tIn\t\tOut" << endl;
    for(int l = 0; l < V; l++)
    {
        cout << l << "\t\t"
             << in_degree[l] << "\t\t" 
             << out_degree[l] << endl;
    }
}

int main()
{

   Graph g(4);
   g.add_edge(1, 0);
   g.add_edge(0, 2);
   g.add_edge(2, 1);
   g.add_edge(0, 3);
   g.add_edge(1, 3);
   g.add_edge(2, 3);


   g.count_in_out_degree();
   return 0;
}

Output:

Vertex		In		Out
0	       	1		2
1	       	1		2
2	       	1		2
3	       	3		0