Given a 2d matrix, filled with 1 and 0. Find the maximum sub-matrix that has only 1’s and return the area.

Given matrix:

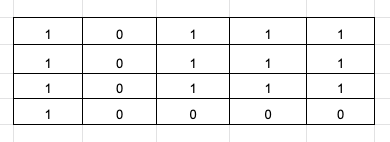
Maximum sub-matrix:

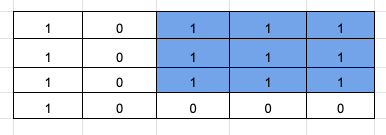
To solve this problem, we shall use Dynamic Programming.

For the given M * N matrix, we shall take another M * N matrix to fill the data. We shall call that array as dp_arr[m][n].
Then when filling each element in the matrix, if the value of the element is 1, then we take the minimum of top, diagonal and left and add 1 to it.

For example:

For the element arr[0][0] is 1. Hence we take min_of(top, diagonal, left) + 1. Here all the values are 0. Hence dp_arr[0][0] = 1.

For the element arr[0][1] is 0. As the element is 0, we put 0 as it is.

For the element arr[0][2] is 1. Hence we take min_of(top, diagonal, left) + 1. Here top = 0, diagonal = 0, left = 0. Hence dp_arr[0][1] = 1.

For the element arr[0][3] is 1. Hence we take min_of(top, diagonal, left) + 1. Here top = 0, diagonal = 0, left = 1. Min is 0. Then add 1, hence dp_arr[0][3] = 1.

For the element arr[0][4] is 1. Hence we take min_of(top, diagonal, left) + 1. Here top = 0, diagonal = 0, left = 1. Min is 0. Then add 1, hence dp_arr[0][4] = 1.

At the end of 1st iteration, our dp_arr will look like below:

Similarly, after 2nd iteration the dp_arr will look as below
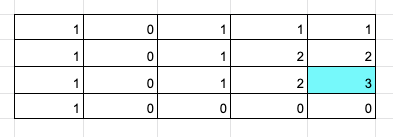
when you reach arr[1][3], here top =1, diagonal = 1, left = 1; hence minimum is 1. Then add 1 to it. The value will become 2. Here top, diagonal and left are highlighted in light green color. Result is highlighted in yellow color.

when you reach arr[1][4], here top =1, diagonal = 1, left = 2; hence minimum is 1. Then add 1 to it. The value will become 2.

By solving we get the final result as 3.
As shown in image below:

Solution in C++

#include<vector>
#include<iostream>
using namespace std;


int get_max_sub_matrix_using_dp(vector<vector<char>>& input)
{	
	int maxSize = -1;

	int row_len=input.size();

	int col_len=input[0].size();

	// initialize dp_arr to 0
	vector<vector<int>> dp_arr(row_len+1,vector<int>(col_len+1,0));

	for(int i=1;i<=row_len;++i)
	{
		for(int j=1;j<=col_len;++j)
		{
			if(input[i-1][j-1]=='1')
			{
				// as "min" will compare only 2 at a time, we 
				// calculate min 2 times.
				dp_arr[i][j]=min(min(dp_arr[i-1][j-1],dp_arr[i-1][j]),dp_arr[i][j-1])+1;

				//we need to get max size, hence we compare present max and stored max.
				maxSize=max(maxSize,dp_arr[i][j]);
			}
		}
	}
	return maxSize*maxSize;
}


int main()
{
	vector<vector<char> > input = { { '1','0', '1', '1', '1' },
                                   { '1', '0', '1', '1', '1' },
                                   { '1', '0', '1', '1', '1' },
                                   { '1', '0', '0', '0', '0' }
                                  };

    int max_sub_martix = get_max_sub_matrix_using_dp(input);

    cout<<"The maximum sub matrix size is "<<max_sub_martix<<endl;
	return 0;

}

The maximum sub matrix size is 9