Get the nth Fibonacci Number

Problem Statement:

You are given a number, you need to find the sum of the 2 preceding Fibonacci sequence.

F(n) = F(n-1) + F (n-2)

Example

Input : n = 2
Output: 1

F(2) = F(1) + F(0) = 1 + 0 = 1

Solution

We can solve this problem by:

1. Recursion
2. Top down approach
3. Bottom Up approach

1. Recursion

We can solve this by recursion.

If n = 4, the recursion tree is as below:

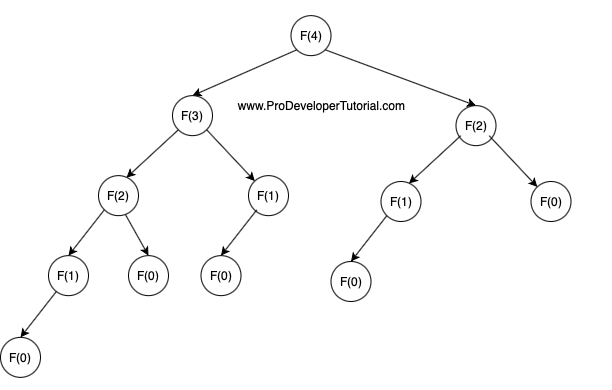
We can define recurrence relation as below:
fib(N-1) + fib(N-2);

2. Top down approach

We can change the approach to memoization. We will take a temp array to store the intermediate result.

3. Bottom Up approach

We can optimize the space complexity by storing the previous 2 values.

Solution in C++

#include <algorithm>  
#include <iostream>    
#include <string>
#include <queue>
#include <vector>
#include <unordered_set> 
#include <list> 

using namespace std;

int get_n_fib_recursion(int N) 
{
      if(N == 0)  
        return 0;

      if(N == 1)  
        return 1;
      
      return get_n_fib_recursion(N-1) + get_n_fib_recursion(N-2);
}


int get_n_fib_top_down(int N) 
{
    if(N < 2)
        return N;

    int dp_arr[N+1];
    dp_arr[0] = 0;
    dp_arr[1] = 1;

    for(int i=2; i<=N; i++)
        dp_arr[i] = dp_arr[i-1] + dp_arr[i-2];

    return dp_arr[N];
}


int get_n_fib_bottom_up(int N) 
{
    if(N < 2) 
        return N;
  int a = 0, b = 1, c = 0;

    for(int i = 1; i < N; i++)
    {
        c = a + b;
        a = b;
        b = c;
    }
    return c;

}

int main(int argc, char const *argv[])
{
  cout<<"The nth fib using recursion "<< get_n_fib_recursion(4)<<endl;
  cout<<"The nth fib using top down "<< get_n_fib_top_down(4)<<endl;
  cout<<"The nth fib using bottom up "<< get_n_fib_bottom_up(4)<<endl;

  return 0;
}

Output:

The nth fib using recursion 3
The nth fib using top down 3
The nth fib using bottom up 3