Get the maximum sum of values of nodes among all connected components of an undirected graph

Problem Statement:

You are given an undirected graph with connected components.

Every node has a value assigned to it.

You need to get the maximum sum of values of nodes among all connected components of an undirected graph.

Example

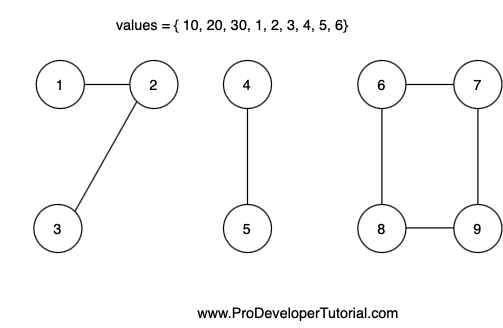
In the above example, there are 3 connected components and the sum of the nodes of 3 connected components are:

Component 1: 10 + 20 + 30 = 60

Component 2: 1 + 2 = 3

Component 3: 3 + 4 + 5 + 6 = 18

Hence the max sum is component 1 i.e 60

Solution

We will use DFS method to get all the connected components.

Then we use “sum” variable to sum up all the values in the connected chain.

At each iteration we check if the sum is greater than the previous sum. If it is greater then we update.

Finally we return the max sum.

Solution in C++

#include <algorithm>  
//visit www.ProDeveloperTutorial.com for 450+ solved questions  
#include <iostream>    
#include <string>
#include <queue>
#include <vector>
#include <stack> 
#include <list> 

using namespace std;

class Graph
{

private:
   int V; 
   list<int> *adj; // to hold adjacency list
   void helper(int v, bool visited[], int& sum, vector<int> node_values ); // helper function for count_max_sum_in_connected_components
public:
   Graph(int V); // Constructor
   void add_edge(int v, int w); // to add an edge to graph
   int count_max_sum_in_connected_components(vector<int> node_values); // returns true if there is a cycle in this graph
};

Graph::Graph(int V)
{
   // get the total number of nodes
   this->V = V;

   // initialize adjacency list for that number of nodes
   adj = new list<int>[V];
}

void Graph::add_edge(int v, int w)
{
   // add the edge to adjacency list
   adj[v].push_back(w); 
   adj[w].push_back(v); 
}


void Graph::helper(int v, bool visited[], int& sum, vector<int> node_values)
{
      visited[v] = true;

      sum += node_values[v-1];

      for(auto i = adj[v].begin(); i != adj[v].end(); i++)
      {
         int adjVertex = *i;

         if ( !visited[adjVertex]){
             helper(adjVertex, visited, sum, node_values);
         }
      }
}

int Graph::count_max_sum_in_connected_components(vector<int> node_values)
{
   bool *visited = new bool[V];
   for(int i = 0; i < V; i++)
   {
      visited[i] = false;
   }
   
   int max_val_sum  = 0;

    for (int v = 0; v < V; v++) 
    {
        if (visited[v] == false) {
            int sum = 0;
            helper(v, visited, sum, node_values);
            if(sum > max_val_sum){
               max_val_sum = sum;
            }
        }
    }
   return max_val_sum;
}


int main()
{
   vector<int> node_values;
   node_values.push_back(15);
   node_values.push_back(25);
   node_values.push_back(35);
   node_values.push_back(45);
   node_values.push_back(55);
   node_values.push_back(65);

   Graph g(6);
   g.add_edge(1, 0);
   g.add_edge(2, 3);
   g.add_edge(3, 4);
   g.add_edge(4, 5);

   int max_sum = g.count_max_sum_in_connected_components(node_values);
   cout << "The max sum of connected components are "<<max_sum<<endl;
   return 0;
}

Output:

The max sum of connected components are 160