Problem Statement:
You are given a directed graph and 2 nodes.
You need to find if there is a path between those two nodes.
Solution
We use BSF to solve this problem.
We take the first vertex as source and perform BSF operation on that vertex.
If we get the second vertex, then there is a path else no.
We use BSF instead of DSF because it is helpful in finding the minimum number of edges between 2 nodes.
Example:
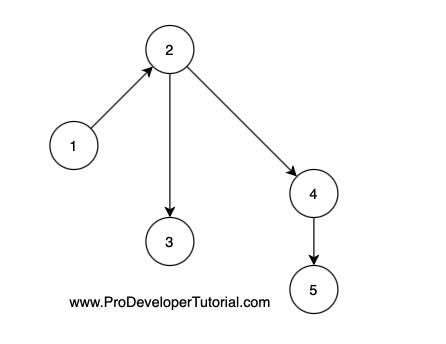
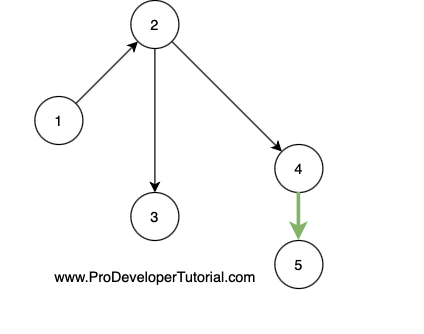
We need to check if there is a path between 1 and 5.
First we take the node 1 and perform BFS operation to node 2
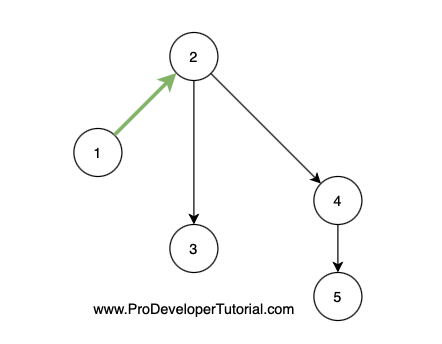
From node 2 to node 3.
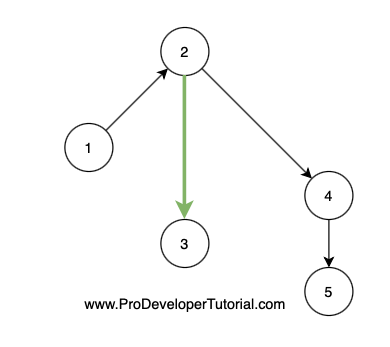
From node 2 to node 4.
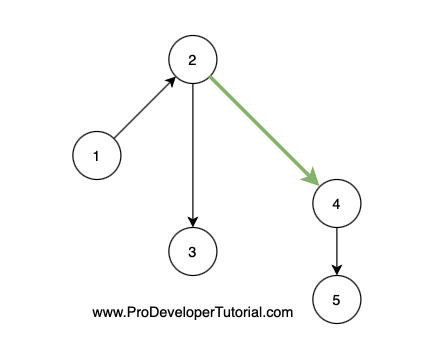
Then from node 4 to node 5
To implement BSF we take help of queue.
Create a queue with the size V.
Start inserting the node into the queue and run a loop until the queue is not empty.
Dequeue the front element and iterate its adjacent elements and push all the adjacent elements in to the queue
If you reach the destination node, then return true else return false.
Time complexity O(V + E)
Solution in C++
#include <algorithm>
//visit www.ProDeveloperTutorial.com for 450+ solved questions
#include <iostream>
#include <string>
#include <queue>
#include <vector>
#include <stack>
#include <list>
using namespace std;
class Graph
{
private:
int V;
list<int> *adj; // to hold adjacency list
public:
Graph(int V); // Constructor
void add_edge(int v, int w); // to add an edge to graph
void print_graph();
bool check_if_is_reachable(int src, int dest);
};
Graph::Graph(int V)
{
// get the total number of nodes
this->V = V;
// initialize adjacency list for that number of nodes
adj = new list<int>[V];
}
void Graph::add_edge(int v, int w)
{
// add the edge to adjacency list
adj[v].push_back(w);
// uncomment below to make the graph as undirected
//adj[w].push_back(v);
}
void Graph::print_graph()
{
for(auto i = 0; i < V; i++)
{
cout<<"\nAdjacency list of vertex "<<i<<endl;
for(auto j = adj[i].begin(); j != adj[i].end(); j++)
{
cout<<" ->"<<*j;
}
}
}
bool Graph::check_if_is_reachable(int src, int dest)
{
if(src == dest)
return true;
bool *visited = new bool[V];
for(int i = 0; i < V; i++)
visited[i] = false;
queue<int> q;
visited[src] = true;
q.push(src);
while (!q.empty())
{
src = q.front();
q.pop();
for (auto i = adj[src].begin(); i != adj[src].end(); ++i)
{
if (*i == dest)
return true;
if (!visited[*i])
{
visited[*i] = true;
q.push(*i);
}
}
}
return false;
}
int main()
{
Graph g(4);
g.add_edge(1, 0);
g.add_edge(0, 2);
g.add_edge(2, 1);
g.add_edge(0, 3);
g.add_edge(1, 3);
g.add_edge(2, 3);
if(g.check_if_is_reachable(1,3)){
cout<<"They are reachable"<<endl;
} else {
cout<<"They are not reachable"<<endl;
}
return 0;
}Output:
They are reachable