Count the ways to decode a digit sequence

Problem Statement:

You are given an digit sequence, you need to count the number of possible decoding of the given digit sequence.

Example

Input: “121”
Output: 3

The possible ways to decode are “ABA”, “AU”, “LA”

Solution

We can solve this problem by using:

1. Recursion
2. Top Down memoization
3. Bottom Up tabulation

1. Recursion:

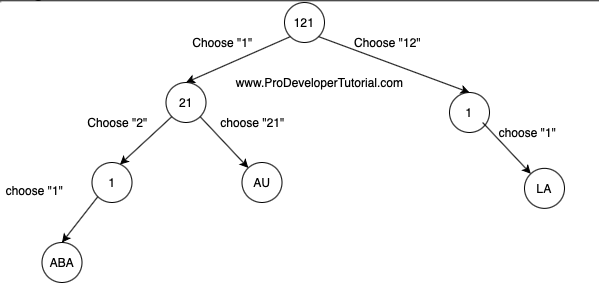
First we will build a tree to see the number of ways the string can be decoded.

We can take a single digit or double digit that is less than 26.

For the above “121” we can make the tree as below

2. Top Down memoization

In this approach we will take an intermediate DP array and store the intermediate result.

We will reduce the time complexity of exponential to linear.

3. Bottom Up tabulation

In the bottom up tabular method, we calculate the number of ways we can decode the string for bottom up.

Means, for example “1112”, we will take array of 5, then for every index we will calculate the number of ways we can decode the string.

Then at the end of the array we will get the result.

The tabular index will be:

1 1 2 3 5

Solution in C++

#include <algorithm>  
#include <iostream>    
#include <string>
#include <queue>
#include <vector>
#include <unordered_set> 
#include <list> 

using namespace std;

int recursion_util(int pos, string& s) 
{
    int n = s.size();
    if(pos == n) 
        return 1;

    if(s[pos] == '0') 
        return 0; 

    int res = recursion_util(pos+1,s);

    if( pos < n-1 && (s[pos]=='1'|| (s[pos]=='2'&& s[pos+1]<'7'))) 
        res += recursion_util(pos+2,s);

    return res;
}

int decode_ways_recursion(string s) 
{
    return recursion_util(0,s);    
}


int top_down_util(int i, string &s, vector<int> &dp_arr) 
{
    if(dp_arr[i]>-1) 
      return dp_arr[i];

    if(s[i]=='0') 
      return dp_arr[i] = 0;

    int res = top_down_util(i+1,s,dp_arr);

    if(i<s.size()-1 && (s[i]=='1'||s[i]=='2'&&s[i+1]<'7')) 
      res+=top_down_util(i+2,s,dp_arr);

    return dp_arr[i] = res;
}

int decode_ways_top_down(string s) 
{
    int n = s.size();
    vector<int> dp_arr(n+1,-1);

    dp_arr[n]=1;

    return top_down_util(0,s,dp_arr);   
}


int decode_ways_bottom_up(string s) 
{
  int n = s.length();

  vector<int> table(s.size()+1, 0);

  if(n == 0 || s[0] == '0')
      return 0;

  table[0] = 1;
  table[1] = 1;

  for (int i = 1; i < s.size(); ++ i) 
  {
      int prev = stoi (s.substr(i-1, 2));
      if (prev == 0) 
        return 0;
      if (prev >= 10 && prev <= 26)  
        table[i+1] += table[i-1]; 
      
      if (s[i] != '0')  
        table[i+1] += table[i];
  }
  return table[n];

}

int main(int argc, char const *argv[])
{
  cout<<"The number of ways to decode using recursion "<< decode_ways_recursion("112")<<endl;
  cout<<"The number of ways to decode using top down "<< decode_ways_top_down("112")<<endl;
  cout<<"The number of ways to decode using bottom up "<< decode_ways_bottom_up("112")<<endl;

  return 0;
}

Output:

The number of ways to decode using recursion 3
The number of ways to decode using top down 3
The number of ways to decode using bottom up 3