Check if undirected graph is connected or not

Problem Statement:

You are given an undirected graph. You need to check if it is connected or not.

Example

Solution

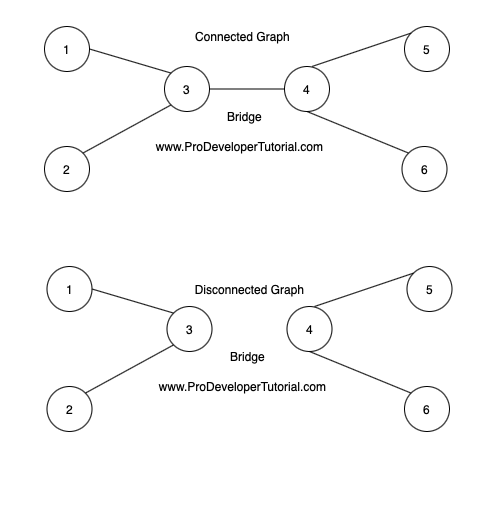
In the above image, the first graph is a connected graph, second is disconnected graph.

In a connected graph, there is always a path from any node to any other node in the graph.

We can solve this problem by using DFS.

We will have a boolean array visited[], then we pick a vertex and visit all the neighboring vertex.

After completion of DFS we check if all the vertices are visited.

Solution in C++

#include <algorithm>  
//visit www.ProDeveloperTutorial.com for 450+ solved questions  
#include <iostream>    
#include <string>
#include <queue>
#include <vector>
#include <stack> 
#include <list> 

using namespace std;

class Graph
{

private:
   int V; 
   list<int> *adj; // to hold adjacency list
   void helper(int v, bool visited[]); // helper function for check_if_connected
public:
   Graph(int V); // Constructor
   void add_edge(int v, int w); // to add an edge to graph
   bool check_if_connected(); // returns true if there is a cycle in this graph
};

Graph::Graph(int V)
{
   // get the total number of nodes
   this->V = V;

   // initialize adjacency list for that number of nodes
   adj = new list<int>[V];
}

void Graph::add_edge(int v, int w)
{
   // add the edge to adjacency list
   adj[v].push_back(w); 
   adj[w].push_back(v); 
}

void Graph::helper(int v, bool visited[])
{

      visited[v] = true;

      list<int>::iterator i;
      for(i = adj[v].begin(); i != adj[v].end(); i++)
      {
         int adjVertex = *i;

         if ( visited[adjVertex] == false ){
             helper(adjVertex, visited);
         }
      }
}

bool Graph::check_if_connected()
{
    bool *visited = new bool[V];
   for(int i = 0; i < V; i++)
   {
      visited[i] = false;
   }

   helper(0, visited);

  for (int i = 0; i <V ; i++) 
  {
      if(!visited[i]){
          return false;
      }
  }

   return true;
}

int main()
{

   Graph g(4);
   g.add_edge(0, 1);
   g.add_edge(0, 2);
   g.add_edge(1, 2);
   g.add_edge(2, 0);
   g.add_edge(2, 3);
   g.add_edge(3, 3);

   if(g.check_if_connected())
      cout << "Graph is connected";
   else
      cout << "Graph is not connected";
   return 0;
}

Output:

Graph is connected