Check if binary tree is a height balanced tree?

Question:

Given a binary tree root node, check if the tree is a height balanced tree.

What is a height balanced tree?

A tree is called as height balanced tree if the difference between left height and right height should not be more than 1.

It means, the value should lie in between (-1, 0, 1).

Example:

Consider the image given below

If we have only 1 node, the height is 0.

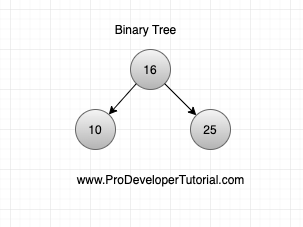
If we have 2 nodes,

Height at root node 16 is 1 – 1 = 0

Consider the image given below

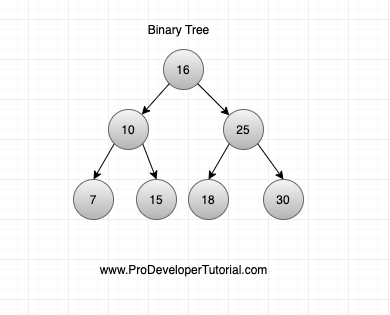
1. Height at node 16 is = right height – left height

right height = 2 and left height = 2.

So height at node 16 is 0.

2. Height at node 10 is = right height – left height

right height = 1 and left height = 1.

So height at node 10 is 0.

Like this we have to calculate the height at each node. If the value is greater than 1, at any node, then that tree is not a height balanced tree.

 

Solution in C++

#include <iostream>
#include <queue>
#include <stack>
using namespace std;

// structure to hold binary tree node
struct Node
{
    int data;
    Node *left, *right;

    Node(int data)
    {
        this->data = data;
        this->left = this->right = nullptr;
    }
};

int is_balanced(Node *node) 
{
    if (node == NULL) 
    {
      return 0;
    }
    
    if(node->left == NULL && node->right == NULL) 
    {
      return 1;
    }

    int lH = is_balanced(node->left);
    int rH = is_balanced(node->right);
    
    if(lH == -1 || rH == -1 || abs(lH - rH) > 1) 
    {
      return -1;
    }

    return max(lH, rH) + 1;
}
  

int main()  
{  
    Node* root = nullptr;
    /* Binary tree:
              16
            /   \
           /     \
          10      25
         /  \    /  \
        /    \  /    \
       7    15 18     30

    */

    root = new Node(16);
    root->left = new Node(10);
    root->right = new Node(25);
    root->left->left = new Node(7);
    root->left->right = new Node(15);
    root->right->left = new Node(18);
    root->right->right = new Node(30);

    if (is_balanced(root))
    {
        cout<<"Binary tree is a balanced tree"<<endl;
    } else {
        cout<<"Binary tree is NOT a balanced tree"<<endl;
  
    }

    return 0;  
}  

Output:

Binary tree is a balanced tree