In this chapter we shall learn about below topics:
10.1 AVL Tree Introduction
10.2 Need of AVL Tree?
10.3 LL Rotation
10.4 RR Rotation
10.5 LR Rotation
10.6 RL Rotation
10.7 Implementation
10.1 Introduction to AVL Tree:
A tree can be called as AVL tree, if it satisfies below 2 properties:
1. It should be a Binary Search Tree
2. The balancing factor should be {-1, 0, 1}
1. The tree should be a BST.
In the previous chapter we have learnt about BST, but we shall see in brief what a BST is.
A tree to be called as BST if the elements to its left are lower than the parent value and the elements to its right are greater than the parent value. And duplicate values are not allowed in BST.
2. The balancing factor:
The balancing factor for every node should be {-1, 0, 1}. The balancing factor for any node can be calculated by below formula:
Balancing_factor = height_of_left_sub_tree – height_of_right_sub_tree.
The result should be either {-1, 0, 1}. The difference is known as balancing factor.
10.2 Need of AVL Trees?
One might wonder, why do we need AVL tree, when we have BST.
Consider the elements {1, 2, 3}. The BST can be constructed in different ways, depending upon the position of the elements.
For example:
1. If the elements are {1, 2, 3} the BST can be as below:
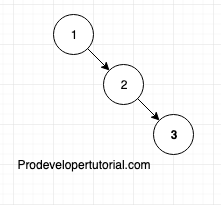
2. If the elements are {2, 3, 1}, the BST will be

3. If the elements are {3,1,2}, BST will be
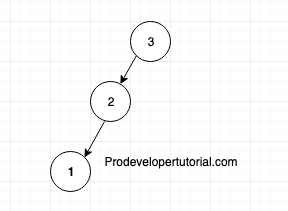
As you see, depending upon the position of the elements, the tree structure changes. But if you use AVL tree, the tree structure will remain same, we shall see further in this chapter.
Ok, now we shall discuss the pervious topic, Balancing factor.
In AVL tree, whenever you insert an element, you need to calculate the balancing factor for all the nodes in the tree. This step is compulsory for every node.
If the balancing factor is not in the range {-1, 0, 1}, then we need to make it balanced.
To make the tree balanced, we have 4 different types of rotation.
1. Left Left Imbalance Rotation
2. Right Right Imbalance Rotation
3. Left Right Imbalance Rotation
4. Right Left Imbalance Rotation
As you might have guessed from above naming convention, we do the rotation depending upon the type of imbalance found. We shall learn about those rotations one by one below:
10.3 Left Left Imbalance Rotation
Consider the elements {3, 2, 1}.
We shall construct AVL tree step by step.
Insert 3

As the node is only 1, the balance factor is 0.
Insert 2
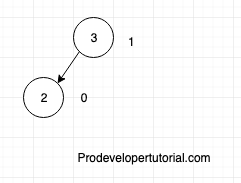
The balance factor for leaf node “2” will be zero. The balance factor for node with value “3” is 1. Because, it has only right child of height 1. Now also it is an AVL tree.
Insert 1.
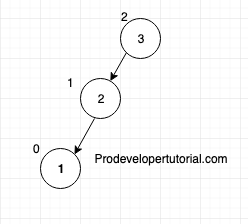
Balance factor for leaf node with value “1” is 0.
Balance factor node with value “2” is 1, as it has only right child
Balance factor node with value “3” is 2, as it has 2 right children. Hence the tree is not balanced.
Observe the image below,
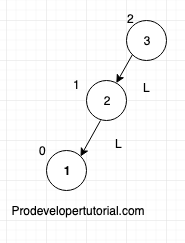
The imbalance has occurred in Left Left child. Hence we say LL rotation. In this case, we need to rotate right side with middle node “2” as root
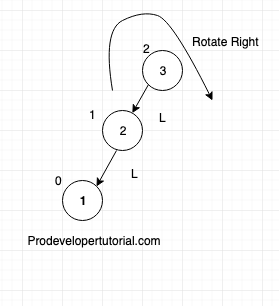
After rotation
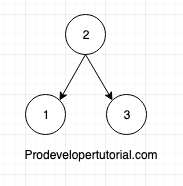
10.4 Right Right Imbalance Rotation
Consider the elements {1, 2, 3}.
Insert 1
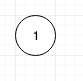
Insert 2
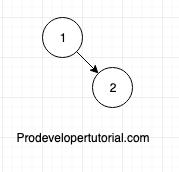
Insert 3
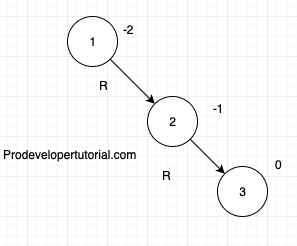
Now there is an imbalance, in Right Right. Hence do a left rotation 2.
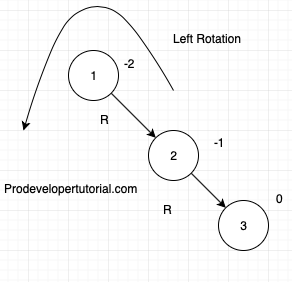
After rotation, final will be
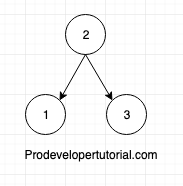
10.5 Left Right Imbalance Rotation
Consider the elements {3, 1, 2}.
The BST will be
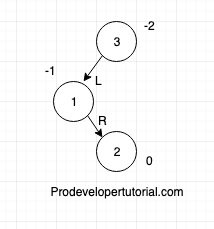
Now you see that there is an imbalance, Left Right imbalance.
To make it AVL balanced, you need to rotate it 2 times. One is Left rotation; another time is Right Rotation.
First rotate left, below is the tree.
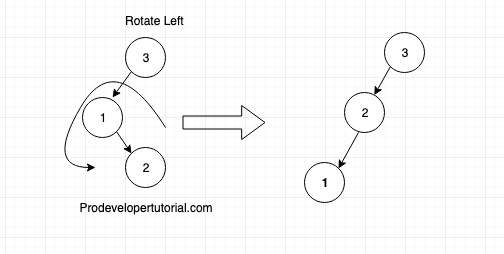
Next rotate Right, below is the final AVL tree.
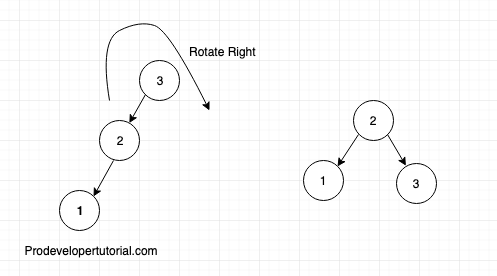
10.6 Right Left Imbalance Rotation
Consider the elements {1, 2, 3}.
The BST will be as below:
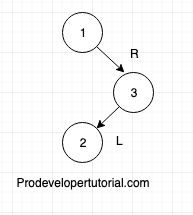
Now you see that there is an imbalance, Right Left imbalance.
To make it AVL balanced, you need to rotate it 2 times. One is Right rotation; another time is Left Rotation.
First rotate Right
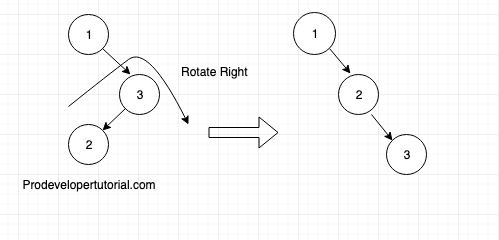
First rotate Left. Below is the final AVL tree.
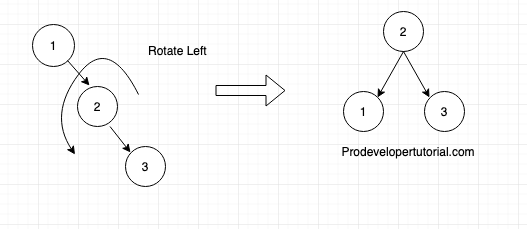
As you see from above 4 rotations, the final AVL tree is the same.
Summary of all the rotations.
Left Left Imbalance Rotation -> Do Right Rotation.
Right Right Imbalance Rotation -> Do Left Rotation.
Left Right Imbalance Rotation -> Do Left rotation, then Right Rotation.
Right Left Imbalance Rotation -> Do Right Rotation, then left Rotation.
10.7 Implementation of AVL Trees
#include "stdio.h"
#include "stdlib.h"
//AVL Tree Node
struct Node
{
int data; // Store the data
int height; //Store the current height of node
struct Node* left; // Link to left child
struct Node* right; // Link to right node
};
//Create a new node
struct Node* NewNode(int data)
{
struct Node* temp = (struct Node*)malloc(sizeof(struct Node));
temp->data = data;
temp->left = NULL;
temp->right = NULL;
temp->height = 1;
return temp;
}
int get_max_height(int a,int b)
{
return (a>b)?a:b;
}
int get_height(struct Node* node)
{
if(node==NULL)
return 0;
return node->height;
}
int Balance(struct Node* node)
{
if(node==NULL)
return 0;
return get_height(node->left) - get_height(node->right);
}
struct Node* LeftRotate(struct Node* a)
{
struct Node* b = a->right;
struct Node* temp = b->left;
b->left = a;
a->right = temp;
a->height = get_max_height(get_height(a->left),get_height(a->right))+1;
b->height = get_max_height(get_height(b->left),get_height(b->right))+1;
return b;
}
struct Node* RightRotate(struct Node* a)
{
struct Node* b = a->left;
struct Node* temp = b->right;
b->right = a;
a->left = temp;
a->height = get_max_height(get_height(a->left),get_height(a->right))+1;
b->height = get_max_height(get_height(b->left),get_height(b->right))+1;
return b;
}
void preorder(struct Node* root)
{
if(root==NULL)
return;
printf("%d ",root->data);
preorder(root->left);
preorder(root->right);
}
struct Node* insert(struct Node* root,int data)
{
if(root==NULL)
return NewNode(data);
if(data < root->data)
root->left = insert(root->left,data);
else if(data > root->data)
root->right = insert(root->right,data);
else
return root;
root->height = get_max_height(get_height(root->left),get_height(root->right))+1;
int balance = Balance(root);
// LL imbalance case
if(balance > 1 && data < root->left->data)
return RightRotate(root);
// RR imbalance case
if(balance < -1 && data > root->right->data)
return LeftRotate(root);
// LR imbalance case
if(balance > 1 && data > root->left->data)
{
root->left = LeftRotate(root->left);
return RightRotate(root);
}
// RL imbalance case
if(balance < -1 && data < root->right->data)
{
root->right = RightRotate(root->right);
return LeftRotate(root);
}
return root;
}
int main()
{
struct Node* root = NULL;
root = insert(root,5);
root = insert(root,10);
root = insert(root,15);
root = insert(root,30);
root = insert(root,14);
root = insert(root,24);
root = insert(root,3);
printf("\nPreorder traversal of tree is : \n");
preorder(root);
return 0;
}
10.8 Output
Preorder traversal of tree is :
15 10 5 3 14 30 24