Arrays: Inversion Count in an Array

Problem Statement:

You are given an unsorted array, you need to return the inversion count.

Inversion count is the number of swaps required to make the array as sorted.

If the input array is already sorted, then inversion count is 0.

Example 1:

arr[] = {3, 1, 2}
Output: 2

Because, the above array can be sorted by making 2 inversions as : (3, 1), (3, 2)

Example 2:

arr[] = {4, 1, 3, 2}
Output: 4

Because the above array can be sorted by making 4 inversions as:(4,1), (4,3), (4,2) and (3,2).

Generally if there are two elements arr[i] and arr[j] form an inversion if arr[i] > arr[j] and i < j

Solution:

This problem can be solved by many different ways. Some of the ways are discussed below:

1. Brute Force Approach
2. Divide and conquer approach [Modified Merge Sort]

1. Brute Force Approach:

In this approach, we check all the elements that is smaller than the current element towards its right side and take the count.

We do this for all the elements and we get the final count

Let us understand this approach with the help of an example:

Consider the example [3, 2, 1].

First we take 3 and check the number of elements lesser than 3 towards its right. We have {3, 2}, {3, 1}

Then we move to the next element “2” and check the number of elements less than “2” towards its right. {2, 1}

So the total count is 3.

The total time complexity for this approach is O(n^2).

Solution in C++

#include <vector>    
#include <algorithm>  
//visit www.ProDeveloperTutorial.com for 450+ solved questions  
#include <iostream>    
#include <queue>

using namespace std;  


int inversion_count(int arr[], int size)
{
    int inv_count = 0; 
    for (int i = 0; i < size - 1; i++)
    { 
        for (int j = i + 1; j < size; j++)
        {
            if (arr[i] > arr[j])
            { 
                inv_count++; 
            }
         }
      }
  
    return inv_count; 
}

int main() 
{ 
    int arr[] = {3, 2, 1};  

    cout<<"The inversion count is "<<inversion_count(arr, 3)<<endl;

    return 0; 
}

Output:

The inversion count is 3

2. Divide and conquer approach [Modified Merge Sort]

This approach is very much similar to merge sort.

We divide the array into individual elements, then while merging the elements, we take the count of the elements that are larger than the current element towards its right.

We shall understand with the help of an example.

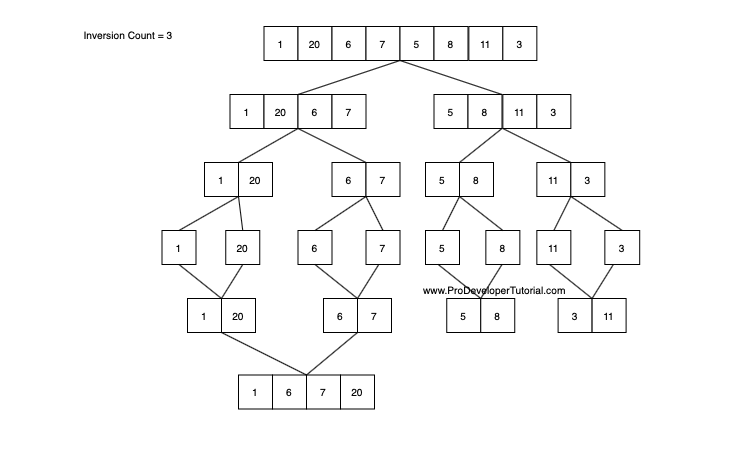
Consider the array [1, 20, 6, 7, 5, 8, 11, 3]

First step is to divide the array. The final divided array will look as below:

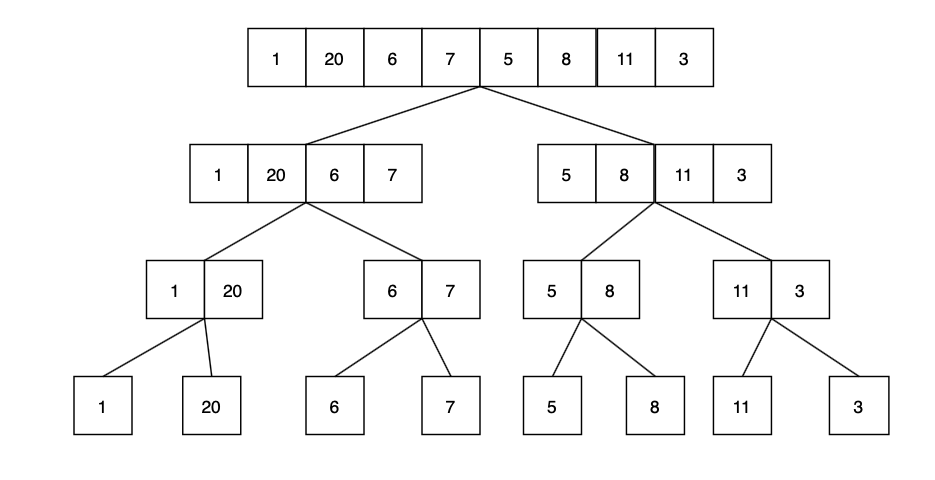
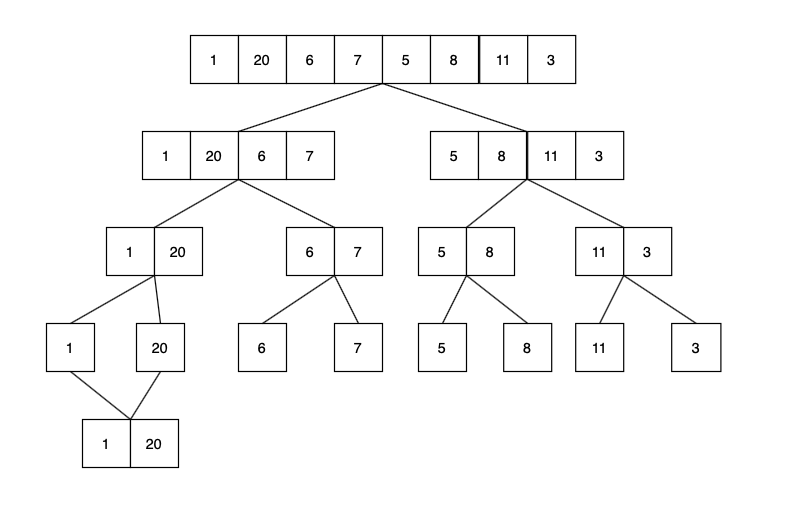
Now we start merging it, we shall start merging in ascending order.

The first merge [1, 20] there will be no increase in inversion count.

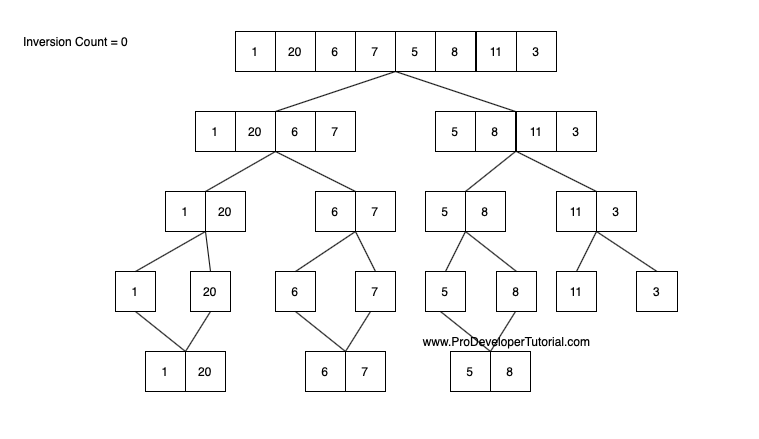
Now after this, we look at the next set [6, 7], 6 is lower than 7 and is on LHS. Hence we will not increase inversion count.

Now after this, we look at the next set [5, 8], 5 is lower than 8 and is on LHS. Hence we will not increase inversion count.

Now after this, we look at the next set [11, 3], 11 is greater than 3 and is on LHS. Hence we will increase inversion count. And merge in ascending order.

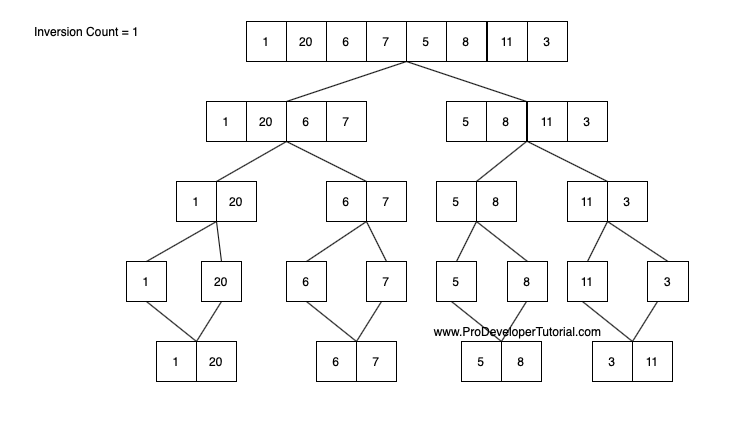
First level merging is completed. We shall do the 2nd level merging.

In this case, we compare the set [1, 20], [6, 7].

Now we shall check if “1” is lesser than “6”, so we will not increment the inversion count.
Now we shall check if “20” is greater than “6”, hence there is an inversion. But how many inversion count?
The count will be equal to the number of elements RHS to “20”. So we have “6”, “7” at RHS. So the inversion count will be 3.

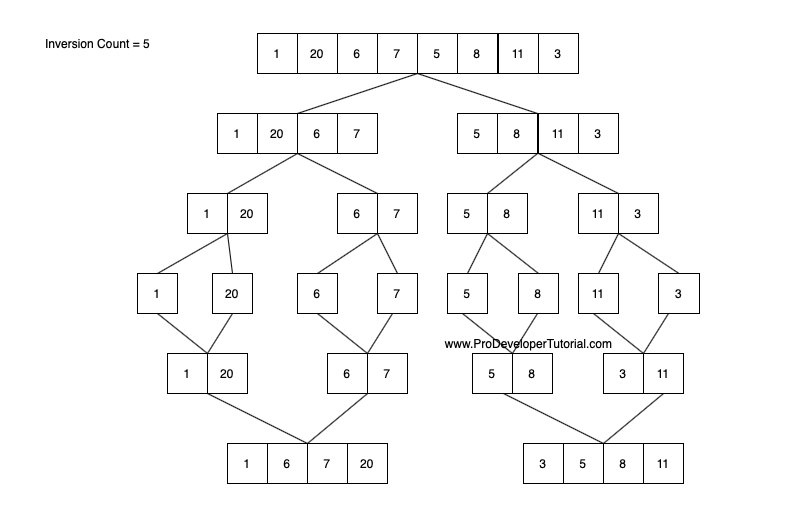
Now we shall look at the set [5, 8], [3, 11]

Now we shall check if “5” is lesser than “3”, it is false. So we will increment the inversion count 2 times as there are 2 elements RHS of 5 i.e “8”, “3”. Total inversion count will be 5.

By following the same procedure, we will get the total inversion count as 13

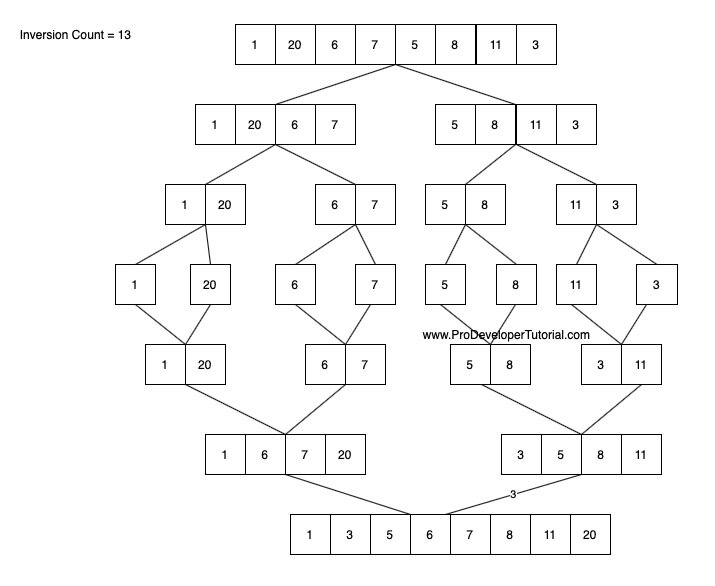
Here the Time Complexity will be O(NlogN)