Graph data structure tutorial 9. Euler Graph

Definition: A graph having Euler Path is called as Euler graph.

Sometimes Euler path is also called as Euler Circuit.

So, what is Euler path or Euler Circuit?

A path which starts and ends at same vertex is called as Euler Path. It means, you need to visit all the edges only one.

Note: A vertex can be repeated but edge cannot be repeated.

Let us understand Euler Graph with help of an example:

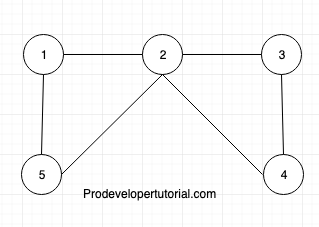
Here we can traverse

1 -> 2 -> 3 -> 4 -> 2 -> 5 -> 1

Here we started at vertex 1 and traversed all the edges only once and ended at vertex 1 again.

Hence this graph has Euler circuit. Hence it is a Euler graph.

Below are the conditions for a graph to be a Euler Graph:

1. All the vertices in the graph should have even degree.

2. A graph has a with vertex with 0 degree, then also it is considered as Euler Graph.

In a graph, if we are able to visit all the edges, but cannot return to the starting vertex is called as semi Euler graph.

Example:

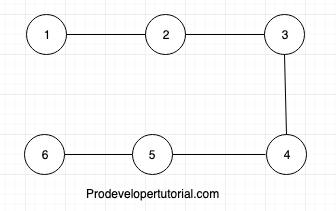
Here we can go from

1 -> 2 -> 3 -> 4 -> 5 -> 6.

Here we have visited all the edges, but did not return at the starting edge. Hence it is a semi Euler graph.

All the vertices have even degree, except for 2 vertices, it will have odd degree.