In this tutorial we shall learn about 2 Colour Graph Problem
In general graph colouring or edge colouring problem we need to assign colour to vertices in such a way that no edge link two vertices with the same colour.
Consider the below set of images:
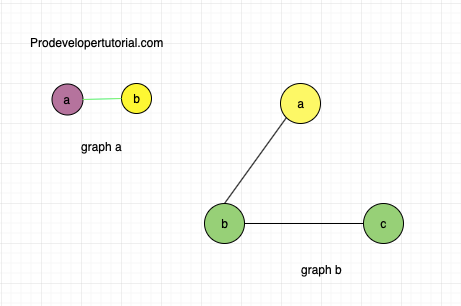
Here graph a is valid. But graph b is invalid because, there is an edge between vertex “b” and vertex “c” that have the same colour.
How to solve this?
A simple solution will be to set each vertex with different colour. But, the goal is to use few colours as possible.
Graph colouring algorithms are used in many areas, including scheduling application.
Now coming to our topic of 2 colour graph problem. What is the need to study this problem now?
In the previous section we learnt about bipartite graph. For a graph to be bipartite it should be a 2 colour graph. Hence if we can prove that a graph can be coloured by only 2 colours, then that graph is a bipartite graph.
So how to colour a graph by using only 2 colours?
It’s simple. Choose a starting vertex, and give it a colour say “red”.
Now make all its neighbour have other colour say “green”.
And all the neighbouring vertex of the “green” colour vertex, colour it “red”.
Continue till al the vertex are coloured.
The image below shows step by step procedure for 2 colour graph problem.
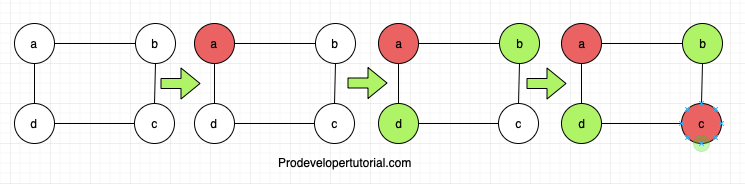
In the above image, we have coloured the graph using only 2 colours.
So to check if the graph is bipartite, we check if the graph is 2 colourable and also it should not contain odd cycle.