Problem Statement:
You are given a number “n”.
You need to return the least number of perfect square number that sum to n.
A number os called as perfect square, if an integer is the square of another integer.
Example:
1, 4, 9, 16
Example
Example 1:
Input: n = 12
Output: 3
Because, 12 can be added as 4 + 4 + 4
Example 2:
Input = 25
Output = 1
There are 4 ways, that a perfect square number sum can be equal to 25.
1. 3^2 + 4^2 => 2 ways
2. 3^2 + 2^2 + 2^2+ 2^2 + 2^2 => ways
3. 1^2 + 1^2 + 1^2 + 1^2 …….. 1^2 + 1^2 + 1^2 + 1^2 => 25 ways
4. 5^2 => 1 way
Here we will choose 5^2 as it is the least number.
Example 3:
Input: 13
Output: 2
To get the sum as 13, we need to add (2^2 + 3^2).
Solution
This problem can be solved by using:
1. Recursion
2. Top Down approach
3. Bottom Up approach
Before we start the solution we will understand below points.
1. First we will check if the number itself is a perfect square. Then we return 1.
2. If N <= 3, then we will return N.
Because we can split 1, 2, 3 with perfect square of 1 only.
N = 1 => 1^2 => 1 way
N = 2 => 1^2 + 1^2 => 2 ways
N = 2 => 1^2 + 1^2 + 1^2 => 3 ways
The above will be the base case.
Then if we have a number “7”. We need to split at the numbers that are perfect square.
First we split at 1^2 i.e 1, then we need to calcualte the split for(7-1) = 6. Next we need to check in how many ways we can split “6” such that the number is a perfect square.
Else if we split at 2^2 i.e 4, then we need to calculate the split for (7-4) = 3. We need to calcuate the number of ways that we can split 3 such that the number is a perfect square.
We cannot split at 3^2 i.e 9 because it is out of bounds.
For that we can write the for loop as:
for(i = 1; i*i <= N; i++) // here i*i is the out of bounds condition.
ans = min(ans, 1+solve(N- i*i)) // here we are subtracting i*i from N, as we need to split at perfect square number.
1. Recursion
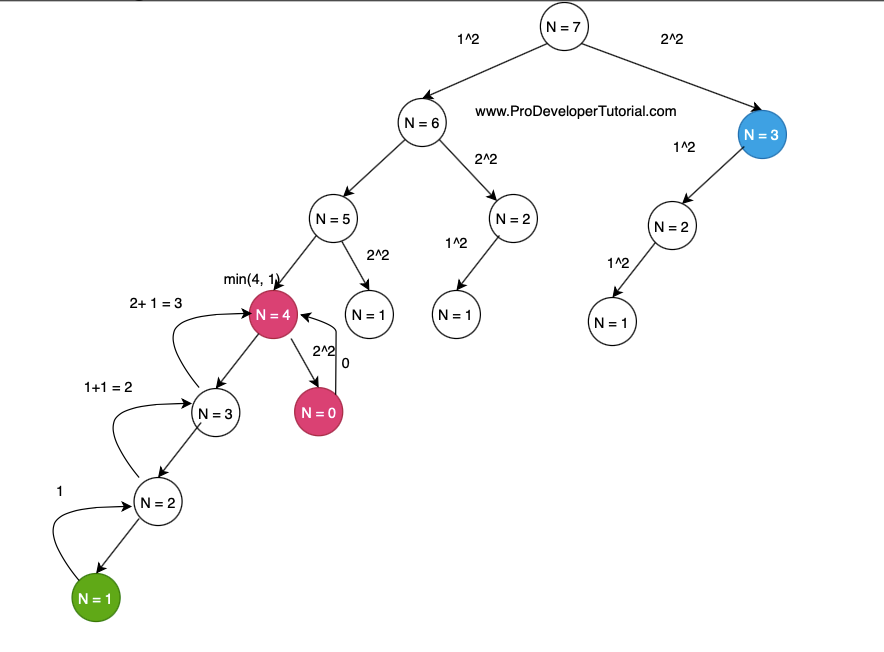
For N = 7 the recursion tree is as below:
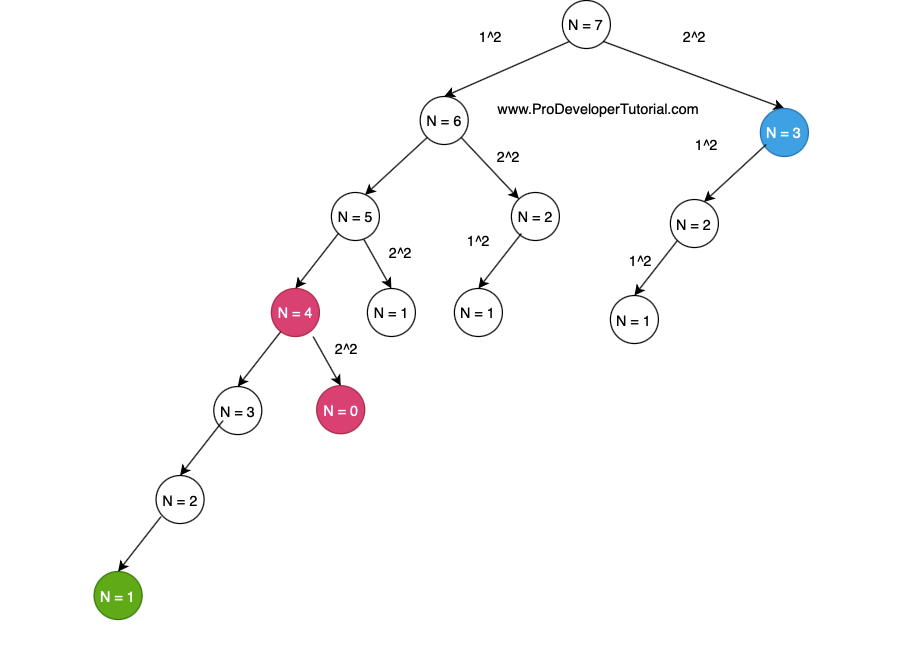
From the above image, once we reach N = 1 (green node), we return 1, as it is the base case.
Then when we reach “N = 2”, we return 1, so it will add to the previous result so it will be 2.
When “N = 3” we return 2+1 = 3 ways.
Once we areach ” N = 4″, 4 is a perfect square. So there is 1 way. So we take the min of (3+1, 0+1) = 1.
Similarly we return the values as below:
2. Top Down approach
We can reduce the time complexity from exponential to linear, by taking a temp array that will store the intermediate results.
3. Bottom Up approach
We can solve this problem by using Bottom up approach.
We build the base case and from there we move towards the solution.
WKT if N <= 3 return N.
If we have N = 6, Below will be our tabular array.
First we will fill the array with the index value, because, any number can be split into the number of 1^2.
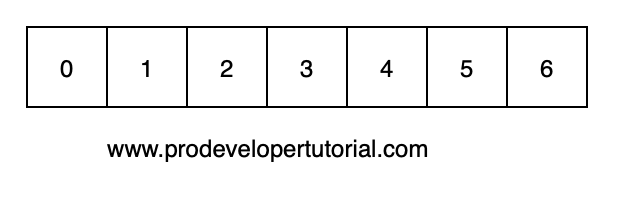
From there we will optimize by using previous values.
We shall start from index 4.
At 4, we shall check if there a number such that it is a perfect square.
There is a number, 2^2.
We can get from below for loop
for(j = 1; j*j <= i; j++)
dp[i] = min(dp[i], 1+dp[i – j*j])
Solution in C++
#include <algorithm>
#include <iostream>
#include <string>
#include <queue>
#include <vector>
#include <unordered_set>
#include <list>
using namespace std;
vector<int> dp;
int top_down_util(int n)
{
if(n<=3)
return n;
if(dp[n]!=-1)
return dp[n];
int ans = n;
for(int i=1;i*i<=n;++i)
ans = min(ans,1+top_down_util(n-i*i));
dp[n] = ans;
return ans;
}
int solve_top_down(int n)
{
dp.resize(n+1,-1);
int ans = top_down_util(n);
return ans;
}
int solve_bottom_up(int n)
{
int tabular[n+1];
tabular[0] = 0;
for(int i=1;i<=n;++i)
{
tabular[i] = i;
for(int j=1;j*j<=i;++j)
{
int sq = j*j;
tabular[i] = min(tabular[i],1+tabular[i-sq]);
}
}
return tabular[n];
}
int main(int argc, char const *argv[])
{
cout<<"The perfect square sum is by using top down "<< solve_top_down(13)<<endl;
cout<<"The perfect square sum is by using bottom up "<< solve_bottom_up(13)<<endl;
return 0;
}Output:
The perfect square sum is by using top down 2
The perfect square sum is by using bottom up 2