Dynamic Programming: Permutation Coefficient

Problem Statement:

you are given 2 numbers n & k, you need to find permutation coefficient.

What is Permutation Coefficient?

Permutation Coefficient is number of ways to order “r” things out of “n” different things.

It means, that if we have n elements and choose “r” elements from it, we need to find the ways of rearranging them.

nPr denotes the ways of doing it

P(n,r) = n!/(n-r)!

Solution

Method 1: Naive approach:

In this method, we use the formula:
P(n,k) = P(n-1, k) + k * P(n-1, k-1)

note:
0! = 1
1! = 1
Complexity O(2^k)

Method 2: DP

As there are overlapping sub problems, we can use Dynamic Programming.

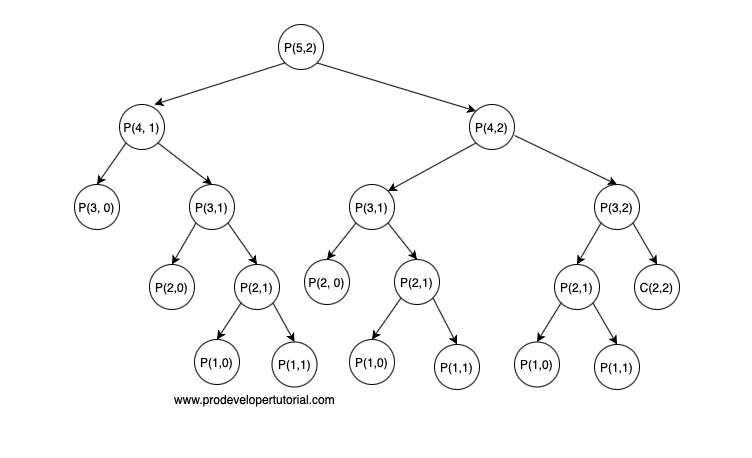
Solution in C++

#include <vector>    
#include <algorithm>  
//visit www.ProDeveloperTutorial.com for 450+ solved questions  
#include <iostream>    
#include <string>
#include <unordered_map>
#include <queue>

using namespace std;


int permutation_coeff_naive_approach(int n, int k)
{
    //Base cases
    if(k==0){
        return 1;
    }
    if(k>n){
        return 0;
    }
    //Recursive call
    return (k* permutation_coeff_naive_approach(n-1,k-1) +
               permutation_coeff_naive_approach(n-1,k));
}

int permutation_coeff_DP_approach(int n, int k)
{

    int P[n+1][k+1];

    for(int i=0;i<=n;i++){
        for(int j=0;j<=min(i,k);j++)
        {

                //Base Cases
                if(j==0){
                    P[i][j]=1;
                }else{
                    P[i][j] = P[i-1][j]+j * P[i-1][j-1];  
                }

                P[i][j+1]=0;
        }
   }
   return P[n][k];
}


int main()
{
    int n = 5, k = 2;
    cout << "Value of P(" << n << ", " << k << ") using naive method is "
         << permutation_coeff_naive_approach(n, k)<<endl;

    cout << "Value of P(" << n << ", " << k << ") using DP method is "
         << permutation_coeff_DP_approach(n, k)<<endl;


    return 0;
}

Output:

Value of P(5, 2) using naive method is 20
Value of P(5, 2) using DP method is 20