Detect a cycle in a directed graph

Problem Statement:

You are given a directed graph.
You need to find out if the graph contains cycle or not.

Example

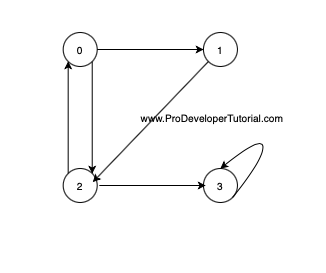
Solution

We shall use DFS to solve this problem:

1. We apply DFS for each vertex and keep track of visiting the vertices in recursion stack.

2. Then if we get a vertex that is already present in recursion stack then there is a cycle.

3. We use visited[] to keep track of already visited vertices.

4. recStack[] is used to keep track of visiting vertices during DFS. We will reset once cycle is not found.

Solution in C++

#include <algorithm>  
//visit www.ProDeveloperTutorial.com for 450+ solved questions  
#include <iostream>    
#include <string>
#include <queue>
#include <vector>
#include <stack> 
#include <list> 

using namespace std;

class Graph
{

private:
   int V; 
   list<int> *adj; // to hold adjacency list
   bool helper(int v, bool visited[], bool *rs); // helper function for check_if_is_cyclic
public:
   Graph(int V); // Constructor
   void add_edge(int v, int w); // to add an edge to graph
   bool check_if_is_cyclic(); // returns true if there is a cycle in this graph
};

Graph::Graph(int V)
{
   // get the total number of nodes
   this->V = V;

   // initialize adjacency list for that number of nodes
   adj = new list<int>[V];
}

void Graph::add_edge(int v, int w)
{
   // add the edge to adjacency list
   adj[v].push_back(w); 
}

bool Graph::helper(int v, bool visited[], bool *recStack)
{

      visited[v] = true;
      recStack[v] = true;

      list<int>::iterator i;
      for(i = adj[v].begin(); i != adj[v].end(); i++)
      {
         int adjVertex = *i;

         // check if the vertex is already visited, if it is not visited
         // then call the helper function.

         if ( !visited[adjVertex] && helper(adjVertex, visited, recStack) )
            return true;
         // if the vertex is visited, then check if is also there in recursion stack
         // if it is there, then there is a cycle
         else if (recStack[adjVertex])
            return true;
      }

   
   recStack[v] = false; // remove the vertex from recursion stack
   return false;
}

  bool Graph::check_if_is_cyclic()
{
    bool *visited = new bool[V];
   bool *recStack = new bool[V];
   for(int i = 0; i < V; i++)
   {
      visited[i] = false;
      recStack[i] = false;
   }

   // call the helper function 
   for(int i = 0; i < V; i++){
      if (helper(i, visited, recStack))
         return true;
   }

   return false;
}

int main()
{

   Graph g(4);
   g.add_edge(0, 1);
   g.add_edge(0, 2);
   g.add_edge(1, 2);
   g.add_edge(2, 0);
   g.add_edge(2, 3);
   g.add_edge(3, 3);

   if(g.check_if_is_cyclic())
      cout << "Graph has a cycle";
   else
      cout << "Graph doesn't have a cycle";
   return 0;
}
/*
   vector<vector<int> > result = combine(n, k);
   cout<<"Result = "<<endl;
   for (int i = 0; i < result.size(); i++)
    {
        for (int j = 0; j < result[i].size(); j++)
        {
            cout << result[i][j] << " ";
        }   
        cout << endl;
    }
    */

Output:

Graph has a cycle