Largest Rectangular Area in a Histogram

Problem Statement:

You are given an array that represents a bar in a histogram.
You need to find out the largest rectangle that can be made from number of continuous bars.

Example

Input = {6, 2, 5, 4, 5, 1, 6}
Output = 12.

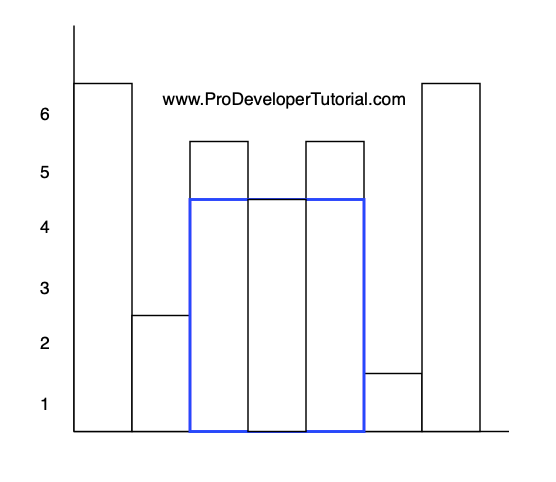
Solution

We shall solve this problem by using stacks.

When we arrive at a index/area, we can expand that area if both left and right height are greater than or equal to the current index.

Then we can include that area.

In our example, when we arrive at index 3, the value is 4. Then we check if all the area besides index 3 is equal to or greater than, then we move to right and left and include those areas also.

So we will start with minimum height. The min height is 1, then we check left and right with less than or equal to the current area.

Then check the area of rectangle with global max and update appropriately.

To know the smaller area to its left and right, we will use stacks.

We add first index into the stack and iterate through the array.

If we get an index/area that is greater or equal to the current top of the stack, we will keep adding them into the stack.

When we get whose height is smaller to the current index, then we will start popping the index out until we get the index whose height is greater or equal to the element to be pushed in.

Then for every popped index, we will calculate the area and compare with global max and update accordingly.

Solution in C++

#include <algorithm>  
//visit www.ProDeveloperTutorial.com for 450+ solved questions  
#include <iostream>    
#include <string>
#include <queue>
#include <vector>
#include <stack> 

using namespace std;

int get_largest_rectangle(vector<int> heights)
{
    int n = heights.size();
    stack<int> s;
    int max_area = 0;
    int area_with_top = 0;
    int top = 0, i = 0;

    while(i < n)
    {
        if(s.empty() || heights[s.top()] <= heights[i])
        {
            s.push(i++);
        }
        else
        {   
            top = s.top();
            s.pop();
            // heights[top] = fully included bar
            // heights[i] = nearest right bar with height < current bar
            // heights[s.top()] = nearest left bar with height < current bar
            area_with_top = heights[top] * (s.empty() ? i : i - s.top() - 1);
            max_area = max(max_area, area_with_top);
        }
    }

    while (!s.empty())
    {
        top = s.top();
        s.pop();
        // s.empty() means it is the smallest bar 
        area_with_top = heights[top] * (s.empty() ? i : i - s.top() - 1);
        max_area = max(max_area, area_with_top);
    }

    return max_area;
}
 
int main()
{
    vector<int>  heights = {6, 2, 5, 4, 5, 1, 6};
    cout << "Maximum area is " << get_largest_rectangle(heights);
    return 0;
}

Output:

Maximum area is 12