Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.
Input: [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6Before solving this problem, please take a look at “Container with most water” problem. There I have explained in detail on how two pointers works.
https://www.prodevelopertutorial.com/find-the-container-with-most-water-explanation-with-diagram-and-solution-in-cpp-language
The above input can be visualized as below:

From the above image the green bars represent the height of the bars given in the input.
The solution for the question is to find the number of places that can hold the rain water. In the image, the blue box represents the water storage. Adding them together we get the output 6.
This problem can be solved in many different ways. Namely:
1. Brute force
2. Dynamic Programming
3. Stacks.
4. Two Pointers
Here we shall discuss about 3 solutions.
1. Brute Force
2. Two Pointers
3. Dynamic Programming
Brute Force Solution:
In this solution we check how much water will be stored in each individual bar, then take the sum of all the individual element to get the output.
Let us take a simple test case, consider the below image:
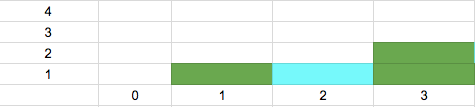
From the image, in the index 0 cannot store any water because it doesn’t have any bar on its left side.
Index 2, it can hold 1 unit of water, because, on its left [index 1] there is a bar height of 1, and on its right [index 3] it is having a bar height of 2.
One more test case:

Here in the index 9, it can store 1 unit of water. Because, Index 8 is of height 2 and index 10 is of height 2.
From the above test cases, we can come to a conclusion that:
area = min(left_max, right_max) – own bar height.
Hence by using this formula, we calculate the area of water stored for each bar and calculate the sum at the end.
General pseudo code:
For each element in the array:
Calculate left_max from the index of that element
Calculate right_max from the index of that element
area += min(left_max, right_max) – own_height[i];
Coming to our problem:
Pass 1:
left_max = 1 right_max = 3 total_area = 0
Pass 2:
left_max = 1 right_max = 3 total_area = 1
Pass 3:
left_max = 2 right_max = 3 total_area = 1
Pass 4:
left_max = 2 right_max = 3 total_area = 2
Pass 5:
left_max = 2 right_max = 3 total_area = 4
Pass 6:
left_max = 2 right_max = 3 total_area = 5
Pass 7:
left_max = 3 right_max = 3 total_area = 5
Pass 8:
left_max = 3 right_max = 2 total_area = 5
Pass 9:
left_max = 3 right_max = 2 total_area = 6
Pass 10:
left_max = 3 right_max = 2 total_area = 6
The total amount of water trapped is 6
Two pointer:
In brute force approach, we used to iterate 2 times to get left_max and right_max for each element. But this can be reduced by using 2 pointers approach. One pointer points to the left index, other pointer points to the right index.
The left_pointer moves towards the right side, and right_pointer moves towards the left.
The point where both pointers crosses each other will be the end of the loop.
We take 2 more variables “left_max” and “right_max” to hold left and right maximum height value.
Coming to our example, we shall understand with the help of series of images:
Pass 0:
Initially the left and right pointers value.

Pass 1:
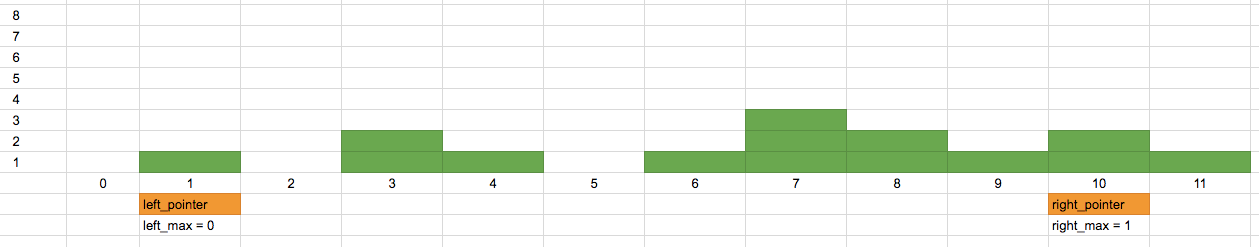
Pass 2:

Similarly, we continue the loop and get the result.
Dynamic Programming:
In the brute force approach, we used to iterate over left_max and right_max every time for a new index to get the values. Instead of repeating everytime, we can store the elements in an array. After that we can use “area = min(left_max, right_max) – own bar height” to get the result.
Solution in C++
/*
* File : trapping_rain_water.cpp
* Author : ajay.thousand@gmail.com
* Copyright: @ prodevelopertutorial.com
*/
#include<iostream>
#include<vector>
using namespace std;
int get_solution_by_brute_force(vector<int>& input_set)
{
int total_area = 0;
int size = input_set.size();
for (int i = 1; i < size - 1; i++)
{
int left_max = 0, right_max = 0;
for (int j = i; j >= 0; j--)
{
left_max = max(left_max, input_set[j]);
}
for (int j = i; j < size; j++)
{
right_max = max(right_max, input_set[j]);
}
total_area += min(left_max, right_max) - input_set[i];
}
return total_area;
}
int get_solution_by_two_pointers(vector<int>& input_set)
{
int left_pointer = 0;
int right_pointer = input_set.size() - 1;
int total_area = 0;
int left_max = 0;
int right_max = 0;
while (left_pointer < right_pointer)
{
if (input_set[left_pointer] < input_set[right_pointer])
{
if (input_set[left_pointer] >= left_max)
{
(left_max = input_set[left_pointer]);
}
else
{
total_area += (left_max - input_set[left_pointer]);
}
++left_pointer;
}
else
{
if (input_set[right_pointer] >= right_max)
{
(right_max = input_set[right_pointer]);
}
else
{
total_area += (right_max - input_set[right_pointer]);
}
--right_pointer;
}
}
return total_area;
}
int get_solution_by_dynamic_programmin(vector<int>& input_set)
{
int total_area = 0;
int size = input_set.size();
vector<int> left_max(size), right_max(size);
left_max[0] = input_set[0];
for (int i = 1; i < size; i++)
{
left_max[i] = max(input_set[i], left_max[i - 1]);
}
right_max[size - 1] = input_set[size - 1];
for (int i = size - 2; i >= 0; i--) {
right_max[i] = max(input_set[i], right_max[i + 1]);
}
for (int i = 1; i < size - 1; i++)
{
total_area += min(left_max[i], right_max[i]) - input_set[i];
}
return total_area;
}
int main()
{
vector<int> input_set;
input_set.push_back(0);
input_set.push_back(1);
input_set.push_back(0);
input_set.push_back(2);
input_set.push_back(1);
input_set.push_back(0);
input_set.push_back(1);
input_set.push_back(3);
input_set.push_back(2);
input_set.push_back(1);
input_set.push_back(2);
input_set.push_back(1);
//int result = get_solution_by_brute_force(input_set);
//int result = get_solution_by_two_pointers(input_set);
int result = get_solution_by_dynamic_programmin(input_set);
cout<< "The total amount of water trapped is "<<result <<endl;
return 0;
}