Input:
Array = [2,3,6,7], key = 7,
Output:
[
[7],
[2,2,3]
]Example 2:
Input: candidates = [2,3,5], target = 8,
A solution set is:
[
[2,2,2,2],
[2,3,3],
[3,5]
]Note: The input array is sorted, with no repeated elements.
Here as there is no time constraint we can solve this example with the help of “backtracking” technique.
First, what is backtracking?
Below is the simplest way that I can explain it to you guys.
When solving a problem, we might come to a result that is not acceptable because of a wrong decision.
Then we have to go back to the step where we have made the wrong decision and try something else.
This is called Backtracking.
Example:
Let’s consider a maze example, where the problem is to find the path between Point A to Point B.
Here while going through the maze, we make a decision and we might get to a dead end. Then we take a step back and take different decision and proceed with it. While we make a wrong decision, we save that decision so that we don’t make the same decision again.
Usually backtracking is associated with recursion. Hence novice programmers will find it difficult to understand. Hope the above explanation has given an introduction to backtracking.
Coming back to our problem:
We perform the below steps to get to the result.
For each number in the set
Step 1: Add the same number until the sum is greater than or equal to that of the key
Step 2: If it is equal, then save the combination
Step 3: If it is greater, then remove the last added number then go back to step 1, add the other number in the set.
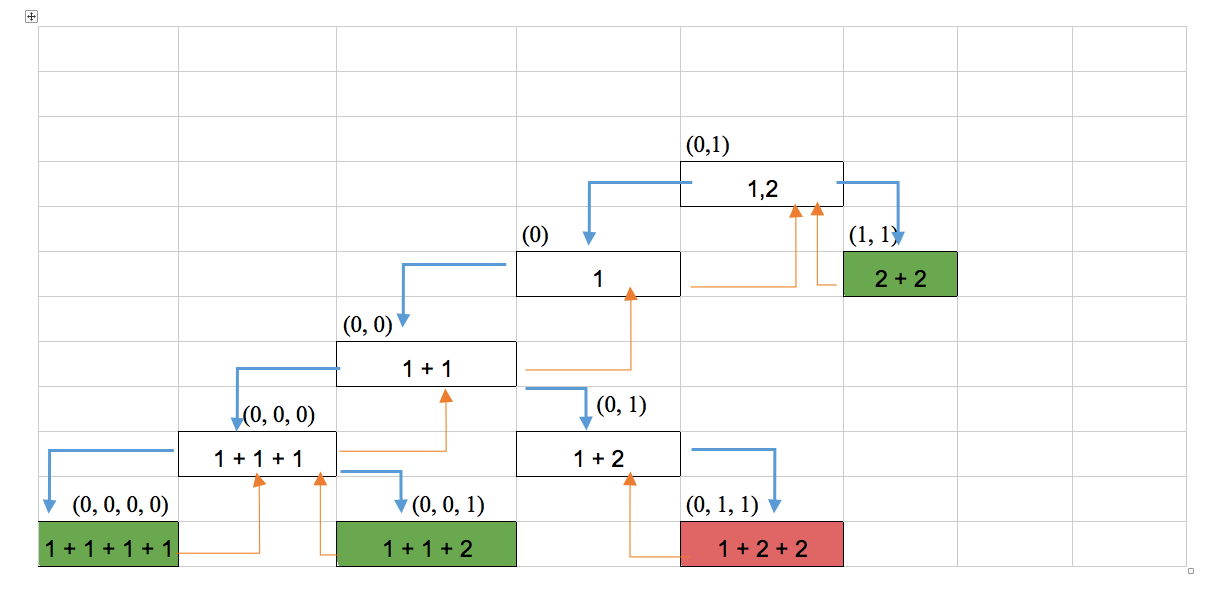
Take the example array [1, 2] and the key = 4.
We get the following steps:
Sum = 1
Sum = 1 + 1
Sum = 1 + 1 + 1
Sum = 1 + 1 + 1 + 1 (sum is same as key, save the combination, remove the last added number and add with the next number from the array)
Sum = 1 + 1 + 1 + 2(sum is greater than key, remove the last added number and add with the next number from the array)
Sum = 1 + 1 + 2(sum is same as key, save the combination, remove the last added number and add with the next number from the array)
Sum = 1 + 2
Sum = 1 + 2 + 2
Sum = 2
Sum = 2 + 2 (sum is same as key, save the combination)The same can be shown pictorially as below:
The green color suggests that the sum of the pattern is equal to the key, hence going back [shown by orange lines]
The red color suggests that the sum is greater than the key, hence going back.
Note: Once we get the exact combination in step 2, we don’t continue, because we know if we continue further, then the total sum will be exceeding the key value. Hence we go back to the previous step.
Our recursion/backtrack function will take 6 parameters as input:
• An array containing the array of integers, for final result
• An array of input set
• An integer having current position
• An integer holding the current_sum
• An integer having “key” value
• An array having current combination of elements
Our backtrack function prototype will look like below:
void backtrack(vector<vector<int>>& final_result_set , vector<int>& input_set, int current_position, int current_sum, int key, vector<int>& current_combination);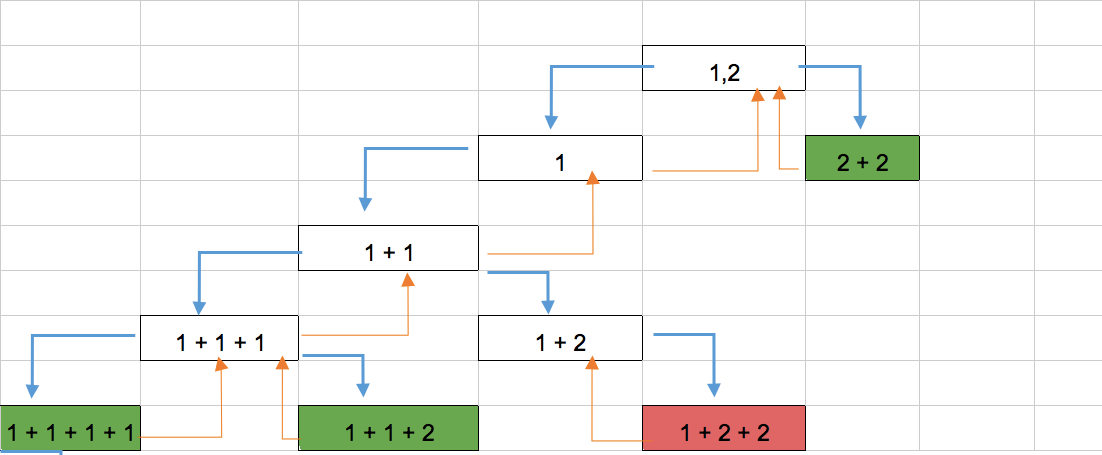
Solution in C++
#include<iostream>
#include <vector>
using namespace std;
void backtrack(vector<vector<int> >& final_result_set , vector<int>& input_set, int current_position, int current_sum, int key, vector<int>& current_combination)
{
if(current_sum > key || current_position == input_set.size()) return;
if(current_sum == key){
final_result_set.push_back(current_combination);
return;
}
backtrack(final_result_set, input_set, current_position + 1, current_sum, key, current_combination);
current_combination.push_back( input_set [current_position]);
backtrack(final_result_set, input_set, current_position, current_sum + input_set[current_position], key, current_combination);
current_combination.pop_back();
}
vector<vector<int> > combinationSum(vector<int>& input_set, int key)
{
vector<vector<int> > final_result_set;
vector<int> current_combination;
backtrack(final_result_set, input_set, 0, 0, key, current_combination);
return final_result_set;
}
int main()
{
vector<int> input_set;
input_set.push_back(2);
input_set.push_back(3);
input_set.push_back(6);
input_set.push_back(7);
int key = 7;
vector<vector<int> > final_set = combinationSum(input_set, key);
// If final_set is empty, then
if (final_set.size() == 0)
{
cout << "No possible combinations found";
return 0;
}
// print the output
for (int i = 0; i < final_set.size(); i++)
{
if (final_set[i].size() > 0)
{
cout << " ( ";
for (int j = 0; j < final_set[i].size(); j++)
cout << final_set[i][j] << " ";
cout << ")";
}
cout<<endl;
}
return 0;
}
Output:
( 7 )
( 2 2 3 )