Problem description:
Given n non-negative integers a1, a2, …, an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.
Solution should be time complexity of O (n) and space complexity O( 1 )
I understand that the question is difficult to understand, below is the explanation so that it can be understood easily.
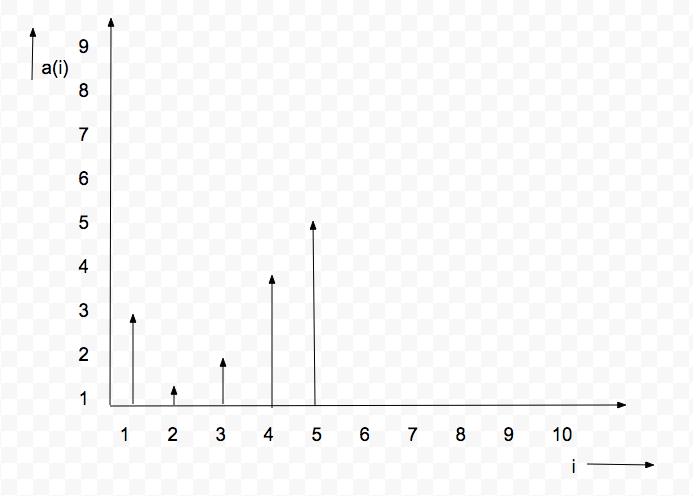
From the diagram it is clear that horizontal line represents “i” and vertical represents “a(i)”. Here in this question, we need to find a container that holds most water.
Input: [3, 5, 4, 6]Output: [15]To find the container that holds the most water, we need to calculate the area of all the container, then we have to take the max of all the area.
To find out the area, we use the below formula:
Area= (right – left) * min (left_height, right_height)
How did we come up with that formula?
Let us analyze with the help of the diagram below.
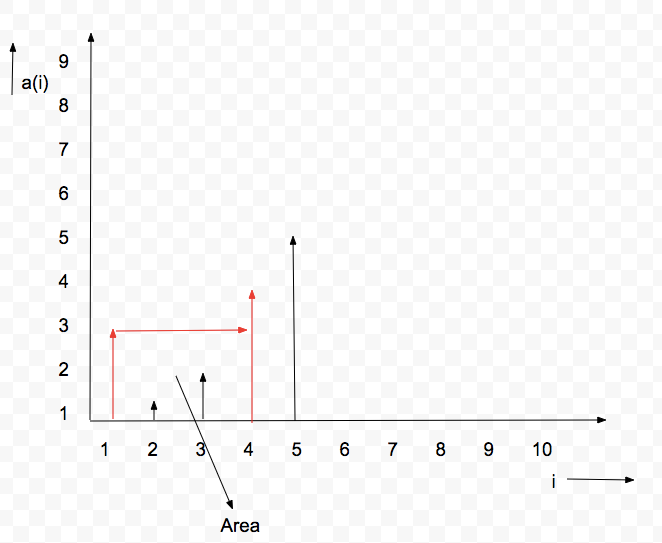
From the diagram, the area is determined by the difference between left and right lines [marked in red]. Since it is a rectangle we need to get the height and width.
Here height is the minimum of the left_height and right_height. We should not take the max height, because it might over flow.
Width will be the distance between the 2 lines. Hence (right – left).
With the help of the above formula we get the area.
Then we get the “max_area” by taking the max value of all the possible container area.
We solve this by taking 2 variables a left_ variable and right_ variable. Left_ variable will start from beginning and right_ variable will point at the end.
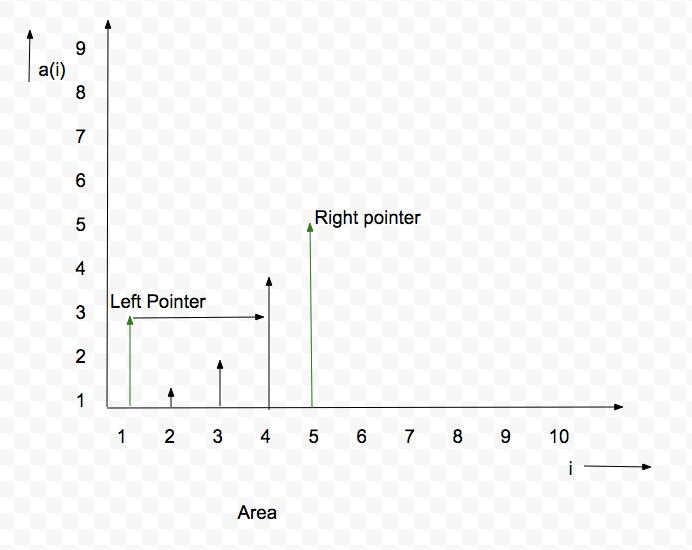
Pseudo code:
while (left_pointer < right_pointer)
{
area = min(arr [left_pointer], arr [right_pointer]) * (right_pointer - left_pointer)
if max_area < area
max_area = area
if (arr[left_pointer] < arr [right_pointer])
left_pointer ++
else
right_pointer ++
}Solution in C++
#include<iostream>
using namespace std;
void calculateMaxContainer(int arr[], int length)
{
int left_pointer = 0;
int rigth_pointer = length -1;
int max_area = 0;
int area = 0;
while (left_pointer < rigth_pointer)
{
// Calculating the max area
// as we have to use constant space of O (1)
// area = min(arr[left_pointer], arr[rigth_pointer]) * (rigth_pointer - left_pointer);
// if (max_area < area)
// max_area = area
// can be written as shown below:
max_area = max(max_area, min(arr[left_pointer], arr[rigth_pointer]) * (rigth_pointer - left_pointer));
if ( arr [left_pointer] < arr [rigth_pointer] )
left_pointer += 1;
else
rigth_pointer -= 1;
}
cout << "The max area is = "<< max_area<< endl;
return ;
}
// Driver code
int main()
{
int a[] = {3, 1, 2, 4, 5};
int length = 5;
calculateMaxContainer(a, length);
}Output:
The max area is = 12