Solution
Before we start with with the solution. Let us understand the basic of DP in series of points as below:
1. DP will be built on top of recursion.
2. So to understand DP you need to first find the recursion solution and from there you can move to DP.
3. We can identify if a question is DP or not by below points:
a. We can divide the problem into overlapping sub problems
b. Optimal solution. It means if you can solve the sub problem optimally, it is guaranteed that you will arrive at the main solution optimally.
Optimal solution question can be like: Min value, Max value, largest etc. So those questions can be solved optimally.
4. One thing to understand, all recursion problems cannot be DP. Because a recursion problem to be a DP, it should have over lapping sub problems.
Then how to identify recursion problem is a DP or not?
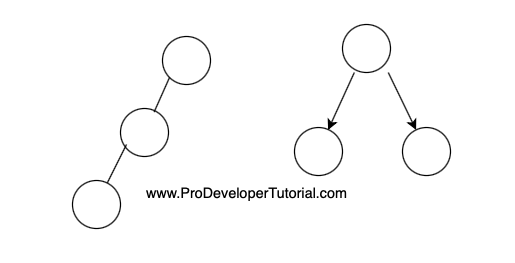
We can identify if in the recursion solution is DP, we should be having choices in the solution.
For example, in the left side recursion tree, there are no choices, so it cannot be a DP. In the right side recursion tree, there are choices, and there might be sub sub problems that are overlapping.
So first we need to find the recurrence relation for the problem, then we can convert the problem into recursion and then we can convert the problem into DP.
Now we have basic understanding of recursion and its relation with DP, we shall solve the problem.
First we shall solve Knapsack with recursion from there we shall evolve to DP.
1. Recursion:
To write the recursion code, first we need to define the recurrence relation, then we can write the recursion code easily.
So according to the question, at every index, we have 2 choices. Either we can take the item or we can leave that item.
We can define the choice tree as below:
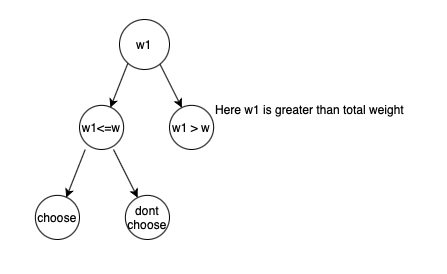
If w1 (weight at index 1) is greater than total weight, we cannot choose it.
If w1 < total weight W, then we can either choose or do not choose it on the basis of, if we get the max profit.
If we choose to include that element, then we need to remove that weight from the total weight.
Then we need to choose other elements with the new weight in such a way that we need to get the max value.
So we can write the recurrence relation as:
max( profit+new weight if we choose the element,
weight if we do not choose the element);
if(w[n-1] <= W)
return max(val[n-1] + knapsack(weight, val, W-w[n-1], n-1),
knapsack(weight, val, W, n-1));
Then for recursion, we need to find the base condition. For that we need to get the smallest valid input.
If we don’t have any item or if the weight is 0 then return 0.
Now we have completed the recursion. We shall learn about Top Down DP.
2. Top Down DP with memoization
Once we arrive at recursive approach, we can change it to Top Down DP with just 2 lines of code change.
From the above explanation it is clear that there are multiple sub problems that we are continuously calculating.
So instead of that, we will take a dp array and initialize it with “-1”.
Then for every step we will store the value in the dp array.
Then during recursion, we will check if the value is filled for that particular cell, if it is filled, then we return the value without doing further computation.
If it is not filled, we will compute the result and update the result in the array.
3. Bottom Up DP with tabular method
In bottom up approach, we start from the base case and build towards the problem.
We will not use recursion here, we will do it linearly.
From the above explanation it is clear that the weight “w” and the items “n” are changing.
Hence we need to create a 2D array with that values.
Point to be noted is that, we need to create a table that is always changing.
Since our W range from 0 to W and range N starts from 0 to N, we need to have total of W+1 * N+1 combinations.
So our 2D array/matrix should be of that size.
Solution in C++
#include <algorithm>
//visit www.ProDeveloperTutorial.com for 450+ solved questions
#include <iostream>
#include <string>
#include <queue>
#include <vector>
#include <unordered_set>
#include <list>
using namespace std;
int max(int a, int b) { return (a > b) ? a : b; }
int knapsack_rec(int W, int wt[], int val[], int n)
{
// base checks
if (n == 0 || W == 0)
return 0;
if (wt[n - 1] > W)
return knapsack_rec(W, wt, val, n - 1);
else
return max( val[n - 1] + knapsack_rec(W - wt[n - 1], wt, val, n - 1),
knapsack_rec(W, wt, val, n - 1));
}
int top_down_util(int W, int wt[], int val[], int i, vector<vector<int>> dp)
{
if (i < 0)
return 0;
if (dp[i][W] != -1)
return dp[i][W];
if (wt[i] > W) {
dp[i][W] = top_down_util(W, wt,
val, i - 1,
dp);
return dp[i][W];
}
else {
dp[i][W] = max(val[i]
+ top_down_util(W - wt[i],
wt, val,
i - 1, dp),
top_down_util(W, wt, val,
i - 1, dp));
return dp[i][W];
}
}
int knapsack_top_down(int W, int wt[], int val[], int n)
{
vector<vector<int>> dp(n+1, vector<int>(W + 1, -1));
return top_down_util(W, wt, val, n - 1, dp);
}
int knapsack_bottom_up(int W, int wt[], int val[], int n)
{
int i, w;
int table[n + 1][W + 1];
for (i = 0; i <= n; i++)
{
for (w = 0; w <= W; w++)
{
if (i == 0 || w == 0)
table[i][w] = 0;
else if (wt[i - 1] <= w)
table[i][w] = max(val[i - 1]
+ table[i - 1][w - wt[i - 1]],
table[i - 1][w]);
else
table[i][w] = table[i - 1][w];
}
}
return table[n][W];
}
int main()
{
int val[] = { 60, 100, 120 };
int wt[] = { 10, 20, 30 };
int W = 50;
int n = sizeof(val) / sizeof(val[0]);
cout << "The max profit using recursion is = "<<knapsack_rec(W, wt, val, n)<<endl;
cout << "The max profit using top down is = "<<knapsack_top_down(W, wt, val, n)<<endl;
cout << "The max profit using bottom up is = "<<knapsack_bottom_up(W, wt, val, n)<<endl;
}
Output:
The max profit using recursion is = 220
The max profit using top down is = 220
The max profit using bottom up is = 220